PHASE CALCULATION AND ITS USE
IN ALLOY DESIGN PROGRAM FOR NICKEL-BASE SUPERALLOYS
H. Harada, K. Ohno, T. Yamagata,
T. Yokokawa, and M. Yamazaki
National Research Institute for Metals
2-3-12 Nakameguro, Meguro-ku, Tokyo 153, Japan
Published in "Superalloys 1988", pp. 733-741,
The Metallurgical Society, 1988.
Abstract
A series of phase calculation equations for gamma and gamma-prime phases in nickelbase superalloys was established by regression analysis on the EPMA data obtained from 30 experimental or commercial alloys together with data from a Ni-Al binary phase diagram. By using these equations, an accurate calculation of gamma/gamma-prime equilibrium, at 900 deg.C, was made possible for various compositions of alloys, from Ni-Al binary to Ni-Co-Cr-Mo-W-Al-Ti-Nb-Ta-Hf-Re multi-component alloys. These phase calculation equations were substituted for those having been used in our alloy design program to extend the applicable composition range and to improve the accuracy of phase and property calculations of the program. Furthermore, a calculation equation for creep rupture life of SC alloys was established and adapted to the program. Using this new version of alloy design, the phase and property were successfully calculated for various types of gamma-prime precipitation hardening nickel-base superalloys.
Introduction
In the design of gamma-prime preoipitation hardening nickel-base superalloys, it is of prime importance to calculate the compositions and fractions of gamma and gamma-prime phases at high temperatures with a high aoeuracy, not only for the prediction of the formation of undesirable phases but also for the further calculations of high temperature properties of the alloys.
Some of the authors previously developed an alloy design program for gamma-prime precipitation hardening nickel-base superalloys [1,2]. By this program, calculations were made possible for gamma/gamma-prime phase equilibrium as well as other structural parameters (e.g., lattice misfit values). Furthermore, high temperature properties, such as creep rupture life and high corrosion resistance, could also be calculated by this program. This program has been successfully applied to the development of conventionally cast (CC), directionally solidified (DS), single crystal (SC), powder metallurgical (PM), and oxide dispersion strengthened (ODS) alloys in national projects of Japan [2-6]. However, this program still had a limitation in the applicable composltion range. For instance, the phase calculatlon was not possible for some existing alloys, such as Alloy 454. This could be attributed to the data for gamma and gamma-prime compositions [7,8] on which our phase calculation equations were established; the compositions were obtained from alloys with various heat treatments and, in addition, the alloy compositions were not widely distributed in the gamma/gamma-prime two phase region. Both of these prevented us from establishing very accurate phase calculation equations between the two phases at high temperature.
This study was performed to reconstruct our alloy design program using our own careful EPMA analysis on experimental and commercial alloy specimens having various compositions which were aged for long times at temperature.
Experimental
Specimens of 20 experimental and l0 commercial alloys, including CC, DS, and SC alloys, were heated at ll00 to 1175 deg.C for 30 hrs after cold work so that gamma/gamma-prime two phase recrystallization occurred to form a coarse gamma/gamma-prime structure. The specimens were then slowly cooled from these temperatures to-900 deg.C and aged for 1500 hrs in order to achieve the equilibrium state at 900 deg.C followed by water quenching.
The specimens thus heat-treated had gamma/gamma-prime lamellar or gamma-prime rod/gamma struotures of 3 to 5 mirons thiokness in both phases. These structures were coarse enough to be analyzed by EPMA with a high acouracy. On the 30 pairs of thus analyzed gamma and gamma-prime compositlons together with a palr from Ni-Al binary phase diagram, regression analysis was carrled out to establish the phase oalculation equations. A series of equations obtained were substituted for those having been used in our alloy design program to improve aacuracy and extend applicable composition range of the program. Furthermore, the calculation of creep rupture llfe of properly heat-treated SC alloys was made possible on the basis of this phase calculation.
Phase Calculation
The gamma + gamma-prime region in multi-component nickel-base superalloys is presented schematically in Fig. 1.
Fig. 1.Schematic phase diagram of multi-component nickel-base super-alloys.
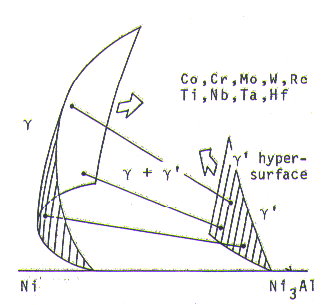
Fig. 2. Relationship between analyzed and calculated Al concentrations in gamma-prime phase.
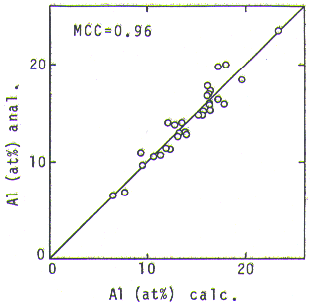
The gamma-prime hypersurraoe in this figure, on which compositions of gamma-prime equilibrated to gamma should be lying, could be expressed by a regression equation, eq.1, where Xi' is a concentration of i-th element in gamma-prime phase.
X'Al = 23.4-0.03.X'Co-0.55.X'Cr-0.71.X'Mo-0.74.X'W
-0.86.X'Ti-0.96.X'Nb-0.48.X'Ta-1.08.X'Hf(-0.74.X'Re) ----- (1)
For this regresslon analysis, the 30 analyzed gamma-prime composltlons were used together with a gamma-prime composition from Ni-Al binary phase diagram at 900 deg.C[9]. sinse the number of alloys containing Re was too small to give a confident coefficient value, the same value as W was used for Re. MCC(Multiple Correlatlon Coefficient) of the equation was 0.96. Although this value was slightly smaller than that of the equation in our previous paper, the value being 0.98, the applicable composition range was found to be remarkably extended. Fig. 2 shows a good agreement between calculated(by eq.1) and analyzed Al concentrations in the gamma-prime phase. The agreement holds in a wide range, from 23.4 at% (in Ni-Al binary alloy) to 6.5 at% (in highly solid solutloned multi-component alloy), whereas the prevlous equation derlved from the data in literature[7,8] tended to give significant amount of error when it was used in a composition range of Ni-Al binary and near to it.
In order to calculate the composition of gamma which is equilibrated to a gamma-prime on the gamma-prime hypersurface, partitioning ratios defined as Ri=Xi/Xi, where Xi is a concentration of i-th element in y phase, are needed. Those of Co, Cr, W, and Al could be well expressed by regression analysis on the 31 pairs of gamma and gamma-prime compositions, as functions of the gamma-prime composition, eqs. 2, 3, 4, and 5. The MCCs were 0.98, 0.92, 0.89, and 0.83, in order. They were increased by 0.07 to 0.13 compared with those in our previous work[2], except W, a
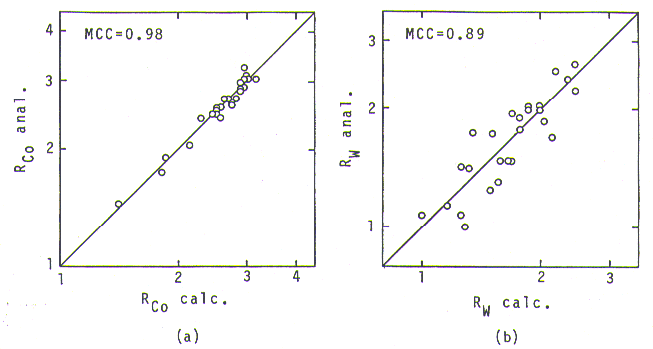
Fig. 3. Relationship between analyzed and calculated partitioning ratios for Co (a) and W (b).
constant value having been used for it. Partitioning ratios of other
elements were found to be well expressed as constants, RMo =3.93, RTi=0.18, RNb=0.30, RTa=0.22, RHf=0.15, and RRe=10.6.
log10(RCo)= 0.529-0.012.X'Co-0.012.X'Cr-0.008.X'W
+0.005.X'Ti ----- (2)
log10(RCr)= 1.429-0.009.X'Co-0.061.X'Cr-0.103.X'Mo
-0.033.X'W-0.016.X'Al ----- (3)
log10(RW)=-0.141-0.015.X'Co+0.052.X'W+0.037.X'Ti
+0.085.X'Nb+0.077.X'Ta ----- (4)
log10(RAl)=-0.274+0.013.X'Co-0.058.X'Mo-0.037.X'W
-0.023.X'Ti-0.087.X'Nb-0.057.X'Ta ----- (5)
Fig. 3(a) shows a good agreement between analyzed and calculated (by eq.2) partitioning ratios of Co; anslyzed ones, distributed from 1.5 to 3, are perfectly expressed by the calculation. In case of W, as shown in Fig. 3(b), the agreement is not as good as with Co, but the equation still expresses the partitioning behavior, the values being distributed from 1 to 2.5. Obviously, using these four equations together with the constant values, the error in phase calculation is expected to be minimized. This is in contrast to PHACOMP [l0] where using constant values for all the partitioning ratios to calculate the gamma and gamma-primey compositions could give a significant amount of error in the result.
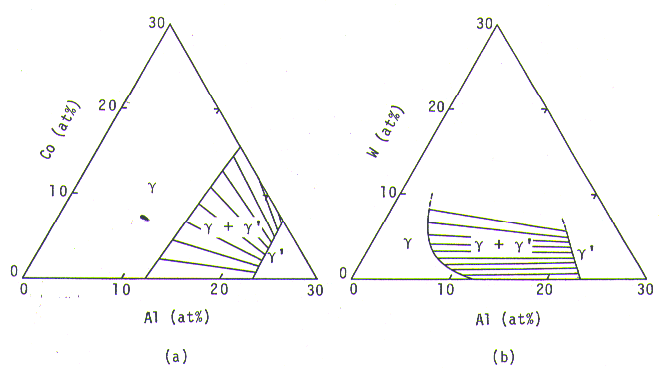
Fig. 4. Calculated gamma +gamma-prime region with tie-lines, at 900 deg.C, for Ni-Al-Co (a) and Ni-Al-W (b) ternary systems.
By substituting the phase calculation equations thus obtained for those having been used in our alloy design program, the efrective range of the program was remarkably extended; this new version could be applied to almost all the gamma/gamma-prime two phase composition range, from Ni-Al binary to Ni-Co-Cr-Mo-W-Al-Ti-Nb-Ta-Hf-Re multi-component systems.
The gamma/gamma-prime equilibrium in Ni-Al-X ternary systems, X= Co, Cr, Mo, W, Ti, Nb, Ta, and Hf, at 900 deg.C, could be successrully calculated by the phase calculation equations. Flg.4 (a) shows the calculation for Ni-Al-Co ternary system. The gamma/gamma-prime region calculated was very consistent with phase diagrams at 800, l000, and 1200 deg.C available from literature[l1]. In Ni-Al-W ternary system, the gamma/gamma-primer region calculated and shown in Fig. 4 (b) was again very consistent with an available phase diagram at 1250 deg.C[12], tielines being not shown in it.
In multi-component alloys, a very good agreement was observed between calculated and analyzed chemical compositions of gamma and gamma-primer phases, examples being shown in Table 1. The first four alloys on the table are alloys included in the 30 alloys used for EPMA analysis and so the agreement in these alloys indicates a good 'interpolation' of the phase calculation. It is to be noted that the calculation for Alloy 454, which was not possible by the old version, becomes possible here. The agreement observed in the last four alloys, whose analyzed data were not used to establish phase calculation equations, indicates a very good 'extrapolation' of the phase calculation in multi-component systems.
From all of these examinations, it was concluded that the gamma/gamma-primer phase equilibrium at 900 deg.C could be calculated by our phase calculation equations with a very high accuracy, for almost all the gamma/gamma-primer two phase composition range, from Ni-Al binary to multi-component alloys.
Table 1.
Comparison between calculated and analyzed chemical compositions of gamma and gamma-primer phases, at 900 deg.C,with atomic fractions (f) of gamma-primer phase calculated from the compositions.
Table 2.
Some or the structural parameters and properties calculated by the new version or alloy design program.
Structural Parameters and Properties
Calculations of other structural parameters,as well as high temperature propertles,were made possible on the basis of the phase calculation mentioned above. The calculation equations established in our previous paper could be successrully used for this purpose after a little modification. The structura1 parameters and properties thus calculated were / density / solubility index(our criterion of phase stability) / PHACOMP parameters / lattice parameters and misfit(at room temperature) / liquidus-solidus temperatures / creep rupture strength(for CC) / tensile properties(for CC, at 900 deg.C) / hot oorrosion resistance(in crucible test at 900 deg.C and burner rig test at 850 deg.C) / and so on.
In addition to these calculations, a calculation of creep rupture life of SC alloys, at 1040 deg.C and at 137MPa, became possible by a regression equation, as a runction of gamma-primer composition, gamma-primer at. fraction, and gamma/gamma-primer lattice misfit. The MCC of the equation was 0.91 when the analysis was carried out using data from our experimental alloys which were cast, heat-treated, and tested in a unified condition. when the data from 6 commercial or xperimental alloys in literature were used together with ours, the MCC reduced
to 0.84. This was probably because of the difference in heat treatment conditions, which will be taken into account in the equation.
It was remarked in both equations that the effect of the lattice misfit,as well as other factors,was found to be very large. The coefficients of the lattice misfit in the equations suggested that the rupture life became longer by factor of 2 or more per every 0.1% change of lattice misfit toward negative(agamma-primeragamma), e.g., from +0.3% to +0.2%. This strongly supported the erfect of large negative lattice misfit on the formation of rafted strueture which increased the creep resistance. Because almost all the alloys used for the regression analysis were expected to have negative lattice misfit values at high temperatures such as 1040 deg.C, the change toward negative at room temperature was very likely to correspond to a change toward larger negative lattice misfit in the negative range at 1040 deg.C.
Table 3.
Output of 'Phase & Property' calculation, for alloy TMS-12, by the
new version of alloy design progranm.
The calculation equation for creep rupture life of SC alloys having MCC of 0.84 was adapted to the alloy design program. Calculation equations for solidus and solvus temperatures were also established on microstructure observation data as functions of the alloy composition, and this was also adapted to the program. An example of the phase & property calculation by this new version of alloy design program is shown in Fig. 5, for Alloy TMS-12, a single crystal alloy developed by the authors using the previous alloy design program.
The calculation was successrully made for various currently used and recently developed alloys, including CC, DS, SC, PM, and ODS alloys. Some of the results are shown in Table II. In the table, TM-321, TMD-5, TMS_1,12, TMP-3, and TMO-2 are alloys designed by authors using previous alloy design program. Alloy SC 83 was designed by Ohno and Watanabe[15], the actual creep rupture life being 3100 hrs at this testing condition. In some SC alloys, the actual creep rupture life was longer than the calculation, probably because of the optimum heat treatments performed for the alloys; MXON, for example,had a life of 1500hrs. It 1s to be noted here that alloy MMT-143 is calculated to have very long rupture life mainly because of the large negative lattice misfit, although the calculation is effective so far as the misfit dislocation is not formed before testing.
Application of the Alloy Design Program
This new version of alloy design program will be used for alloy developments of various types of gamma-prime precipitation hardening nickel-base superalloys, especially the SC alloys, using the calculation equation of creep rupture life as well as all the other calculation equations.
This new version can also be used for quality control of various types of alloys during processing. For example, it is possible to calculate the 'Phase and Property' from the check analysis before tapping the molten metal to make remelt bars or castings and, if needed, one could adjust the chemical composition so that the alloy could exhibit the needed high temperature properties.
Conclusions
1. A series of phase calculation equations for gamma and gamma-prime phases in nickle-base superalloys was established by regression analysls on our EPMA data from 30 experimental or commercial alloys and a data from Ni-Al binary phase diagram.
2. An accurate calculation of gamma/gamma-prime equilibrium, at 900 deg.C, was made possible by using these equations for vasions compositions of alloys, from Ni-Al binary to Ni-Co-Cr-Mo-W-Re-Al-Ti-Nb-Ta-Hf multi-component alloys.
3. A calculation equation for creep rupture life of SC alloys, revealing the strong effect of lattice misfit, could be obtained on the phase calculation and adapted to our alloy design program.
4. Using this new version of alloy design program,phase and property calculation was successrully carried out for various types of gamma-prime precipitation hardening nickel-base superalloys.
Acknowledgment
This work was performed as a part of the R&D project or Basic Technology for Future Industries sponsored by Agency of Intustrial Science and Technology, MITI.
Rererences
[1] H.Harada and M.ramazaki;Tetsu-to-Hagane,65(7)(1979),p.1059(written in Japanese) .
[2] H.Harada, M.Yamazaki, Y.Koizumi, N.Sakuma, N.Furuya, and H.Eamiya; Proo. or Conference, High Temperature Alloys for Gas Turbines 1982, held in Liege, Belgium, 4-6 Oct. 1982, D.Reidel Publishing Co, p.721.
[3] T.Yamagata, H.Harada, S.Nakazawa, M.Yamazaki, and Y.G.Nakagawa; presented at Conference, "5th international Jymposium on Superalloysn, held at Seven 5prings, Pa, Y.S.A., 7-11 Oct. 1984(Proceedings: Superalloys 1984, published by the Metallurgical Society of AIME,p157)
[4] M.Yamazaki; Progress in Powter Metallurgy, vol.41(1986),p.53t.
[5] T.Yamagata, H.Harada, S.Nakazawa, and M.Yamazaki; Trans. Iron and Steel Inst.or Japan, vol.26,(1986),p.638.
[6] T.Yamagata, H.Harada, and M.Yamazakis Proc. of Conference "The 1987 Tokyo International Gas Turbine Congress", held in Tokyo, Japan, 26-31 Oct. 1987, sponsored by Gas Turblne Society of Japan, vol 3, p.239.
[7] O.H.Kriege and J.H.Baris: Trans. ASH, vol.62(1967),p.195.
[8] J.E.Restall and E.C.Toulson: Metals and Materials, March(1973),p.134, April,p.187.(Part 1 and 2).
[9] Constitution of Binary Alloys, 2nd Ed. by M.Hansen and K.Anderko, MoGrow-Hill, New York, 1958. p.119.
[10]R.F.Decker: Symposium on Steel Strengthening Mechanisms, Climax Molybtenum Company, May 1969,Greenwich, Connecticut, U.S.A.,p.147.
[11]J.Schramm, Z.Metallk. vol.33(1941) p.403.
[12] P.Nash, S.Fielding, and D.R.F.West: Met. Sel.,vol.17(1983),p.194.
[13] P.Caron and T.Khan: Mat. Sci. and Engineering, vol.61(1983),p.173.
[14] T.Rhan, P.Caron and C.Duret: presented at Conference, "5th lnternational symposium on Superalloys", held at Seven Springs, Pa, U.S.A., 7-11 Oet. 1984(Proeeedings: Superalloys 1984, published by the Metallurgical Society of AIME,p.145).
[15]T.Ohno and R.Watanabe: Tetsu to Hagane, vol.72, No.13(1986), S1509(written in Japanese).



