COMPUTER ANALYSIS ON MICROSTRUCTURE AND PROPERTY
OF NICKEL-BASE SINGLE CRYSTAL SUPERALLOYS
H.Harada, T.Yamagata, T.Yokokawa,
K.Ohno and M.Yamazaki'
National Research Institute for Metals
2-3-12 Nakameguro, Meguro-ku,
Tokyo l53, Japan
+ Now in Research Development Corporation of Japan
2-5-2 Nagata-cho, Chiyoda-ku,
Tokyo 100, Japan
Published in Proceedings of the Fifth International Conference
held at University College, Swansea, 28th March - 2nd April, 1993, pp. 255-264,
The Institute of Metals.
Abstract
The microstructural parameters and high temperature properties of single crystal (SC) superalloys containing Re, e.g., PWA1484, were examined by our alloy design computer programme.This examination suggested that the lattice misfit change by Readdition is the major factor of the improvement in creep rupture strength in these alloys. The strongest single crystal superalloys available in the Ni-Co-Cr-Mo-W-Al-Ti-Nb-Ta-Hf-Re multi component system were searched for by the same computer programme. Alloys with high Mo and Ta concentrations, having large negative lattice misfit values, were calculated to have highest creep rupture strengths. The Re addition was not necessarily needed to design such ultra-high strength alloys. It was concluded that the control of lattice misfit is of vital importance in designing ultra-high strength SC superalloys.
1. Introduction
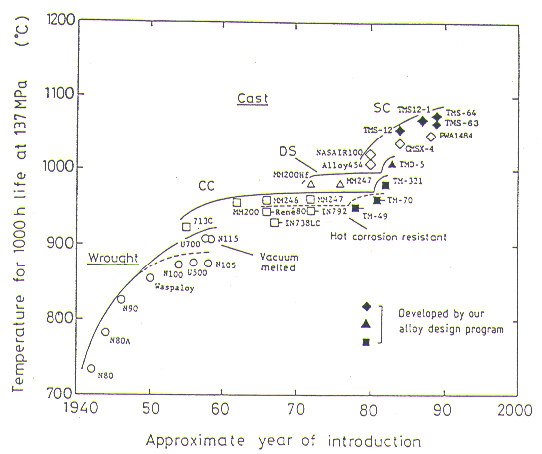
An alloy design computer programme for nickel-base superalloys has been developed and utilised in our alloy development work[1-5]. The temperature capabilities of the alloys developed so far are shown in Fig.1, together with temperature capabilities of commercial nickel-base superalloys. This figure shows that alloys with excellent temperature capabilities have been obtained by the computer programme, especially with single crystal (SC) superalloys. Our latest SC alloys designated as TMS-63 and TMS-64 have relatively small density(About 8.5g/cm3) compared with the other SC superalloys(About 8.9g/cm3 for PWA1484) as well.
In the present study, the same computer programme was employed to examine the microstructural parameters and high temperature properties of so called second generation SC superalloys,e.g., PWA1484, to clarify the factors influencing high temperature strength. A special emphasis was put on investigating the effect of Re additions. An attempt was also made by using the computer programme to search for the strongest single crystal superalloys available in Ni-Co-Cr-Mo-W-Al-Ti-Nb-Ta-Hf-Re multi component system.
Fig.1
Improvement in temperature capability of nickel-base superalloys.
Alloy Design Computer Programme
The schematic flow chart of the alloy design computer programme employed in the present study is shown in Flg.2. The programme is composed of two sub-programmes, namely the analysing programme and the searching programme. The analysing programme was used to calculate microstructural parameters and high temperature properties from alloy chemical compositions. The searching programme was used to find the chemical compositions of the alloys with highest creep rupture strength available in Ni-Co-Cr-Mo-W-Al-Ti-Nb-Ta-Hf-Re multi-component system.
The equations used in the sub-programmes to calculate gamma/gamma-prime equilibrium are same as those derived in our previous work[4]. For the partitioning ratio(gamma/gamma-prime) of Re, the value 10.6 was used. The contribution of Re to the lattice parameter change of gamma and gamma-prime phases was assumed to be the same as that of W. The creep rupture strength is calculated by the equation shown in Table 1. This equation was obtained in our previous work[5] by regression analysis on creep rupture data of 34 SC superalloys.
Fig.2
Schematic flow chart of alloy design computer programme.
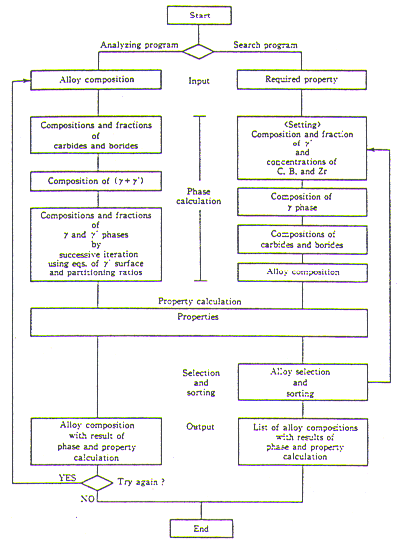
Table 1.
Regression equation for calculating creep rupture life at 1040 deg.C and 137MPa.
Results of Calculation
The result of 'Phase and Property' calculation for PWA1480 and PWA1484 are shown in Table 2. together with that for TMS-63. The keys in the output are explained in Table 3. It is shown in the output that the lattice misfit(LM) in PWA1484 is smaller than that in PWA1480 by 0.34%. This difference is attributed to the addition of Re which is preferentially partitioned to gamma phase and this expands the gamma lattice parameter; this causes lattice misfit to shift in a negative direction.
Although lattice misfit values are positive in almost all the superalloys at room temperature, they are expected to shift in a negative direction when temperature is increased. This is mainly due to the difference in the thermal expansion coefficients of the phases. Our recent X-ray measurements for some SC alloys including TMS-63 showed that the shift is 0.2-0.4% at 1040 deg.C. Thus alloys with smaller positive (or preferably larger negative) lattice misfit at room temperature should have larger negative lattice misfit at high temperatures.
It is known that negative lattice misfit assists the formation of so called rafted structure and increases creep strength at high temperatures[6]. Also if the lattice misfit becomes larger in negative the gamma/gamma-prime interfacial dislocation network becomes finer and this must enhance creep strength at high temperatures by making dislocation cutting into gamma-prime more difficult. As shown in the regression equation in Table 1, the coefficient for lattice misfit is negative; the smaller positive (or larger negative) lattice misfit at RT increases the creep rupture life. This expresses the effect of lattice misfit described above very well.
In our calculation in Table 2, the rupture life of PWA1484(1285 h) is 3.5 times as long as that of PWA1480(370 h) at 1040 deg.C and 137MPa. This is in excellent agreement with the data published by Cetal and Duhl[7]; the improvement in creep rupture life was reported to be as large as factor of 3.7 at 1010 deg.C Alloys CMSX-2 and CMSX-4[8] were also compared with each other in the same way. The result was almost similar to the case of PWA alloys. The lattice misfit in CMSX-4. which contains 3 wt% Re, was smaller by 0.09% compared with CMSX-2. This resulted in an improvement as large as factor of 1.6 in creep rupture life at
Table 2.
Output for PWA1480, PWA1484 and TMS-63, by our alloy design computer programme.
Table 3.
Keys for the computer output shown in Table 2.
Fig.3
Relationship between calculated and experimental creep rupture lives.
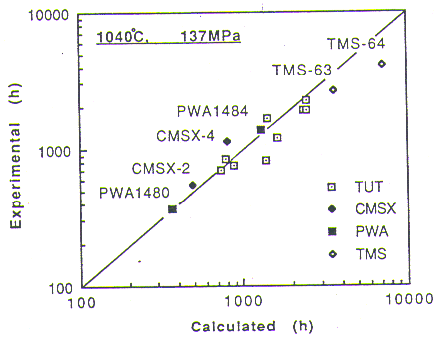
l040 deg.C. These calculations agreed very well with experimental data as shown in Fig. 3.
It has been believed that the excellent temperature capabilities of Re containing superalloys should be attributed to the solid solution strengthening effect of Re in the gamma phase[7]. A micro-clustering of Re in the gamma phase has also been suspected to be the important factor of the improvement[9]. However our calculations described above clearly show that the lattice misfit change caused by Re addition is the major factor of the improvement.
Another calculation was made for a series of alloys having a variety in chemical concentrations in Mo, W and Ta, although concentrations of Cr, Al, Ti and Re were kept constant[10]. As also shown in Fig. 3, calculated creep rupture lives agreed very well with reported experimental data; the error is within a factor of 2. It was also found by the calculation that the strongest alloys, TUT95, TUT92C and TUT31D, had suitable lattice misfit values(0.05 to 0.16% at room temperature) and this is the main reason for the highest creep rupture strengths among the 10 alloys.
Thus the lattice misfit is found to be playing a predominant role on the strengthening of the practical and experimental single crystal superalloys. The effect of solid solution strengthening by refractory elements is also an important factor as seen in the coefficients in the regression equation in Table 1.
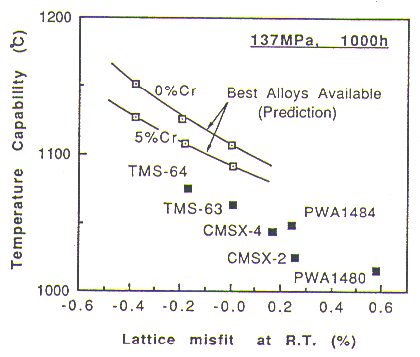
Fig.4
Effect of lattice misfit on the temperature capability of SC superalloys.
However, when we compare alloys fully solid solution strengthened by the refractory elements, difference in the solid solution strengthening level is not so large compared with the difference in the lattice misfit which changes significantly depending upon the combination and balance of the alloying elements.
In fact, not only Re but also Cr, Mo and W are preferentially partitioned to gamma phase to shift the lattice misfit towards negative direction. This means Re is not necessarily needed to design ultra-high strength SC superalloys. This has in fact already been verified by our previous work on TMS-63 and TMS-64[5]. Containing no Re, their temperature capabilities are higher than those of PWA1484 and CMSX-4 by 20 to 30 deg.C since they are automatically designed through the alloy design computer programme to have large negative lattice misfit values at high temperatures. Our recent X-ray measurement up to 1200 deg.C supported our calculation; the lattice misfit in TMS-63 was measured to be larger negative than that of CMSX-4 at high temperatures.
In the series of calculations described above, it was confirmed that our alloy design computer programme gives a very good estimation in both microstructure and high temperature properties. Using this programme, the strongest single crystal superalloys available in the whole gamma/gamma-prime region in Ni-Co-Cr-Mo-W-Al-Ti-Nb-Ta-Hf-Re multi component system were search for. The results of calculation under several selection conditions are summarised in Fig.4.
It is suggested in this figure that the temperature capability can be improved significantly by changing the lattice misfit towards larger negative direction, although there is a limitation in practice. If the lattice misfit is too large, the coherency is easily broken down during heat treatment, even during cooling after solutioning, and creep rupture strength is decreased[6]. Another problem which we found in alloys with too large lattice misfit is a discontinuous coarsening of gamma-prime during creep. We believe this structural change is driven by a large coherent or semi-coherent strain energy at the gamma/gamma-prime interface. Taking these into consideration, the limitation should be set for the lattice misfit at around -0.2S at room temperature. Thus the temperature capability of the strongest alloy with 5% Cr is 1100 deg.C which is higher than that of PWA1484 by 50 deg.C. Reducing Cr below 5S might also be worth considering, since our calculation predicts that it may be possible, for instance, to increase the temperature capability up to 1130C with alloys containing no Cr; this is higher than that of PWA1484 by 80 deg.C.
Conclusions
The single crystal superalloys containing Re, PWA1484, etc., were examined by our alloy design computer programme in terms of the microstructural parameters and high temperature properties to clarify the strengthening mechanism at high temperature. Also the strongest alloys were searched for by the computer programme. Results were as follows.
(1) It is suggested that the lattice misfit change by Re addition is the major factor controlling the improvement of creep rupture strength in Re containing alloys.
(2) The effect of solid solution strengthening by Re, although believed to be responsible for the improvement, was found rather small.
(3) Alloys with high Mo and Ta concentrations as well as large negative lattice misfit values were calculated to have highest creep rupture strengths. The Re addition was not necessarily needed to design ultra-high strength alloys.
(4) The control of lattice misfit was thus found to be of vital importance in designing ultra-high strength SC superalloys.
Acknowledgment
A part of this work was done in "Atomic Arrangement Design and Control Project", a collaborative research project between Research Development Corporation of Japan and University of Cambridge, when one of the authors(H.H) stayed in University of Cambridge, Department of Materials Science and Metallurgy.
References
[1] H.Harada and M.Yamazaki: Tetsu to Hagane,Vol.65,(1979)p.1059.
[2] H.Harada, M.Yamazaki, Y.Koizumi, N.Sakuma, N.Furuya, and H.Kamiya: Proc. of a Conference,"High Temperature Alloys for Gas Turbines 1982", held in Liege, Belgium, p.721.
[3] T.Yamagata,H.Harada, S.Nakazawa, M.Yamazaki and Y.G.Nakagawa: "Superalloys 1984", Proc. of the 6th International Symposium on Superalloys, Seven springs(1984),p.157.
[4] H.Harada, K.Ohno, T.Yamagata, T.Yokokawa, and M.Yamazaki: Proc. of the 6th International Symposium on Superalloys, Seven Springs(1988), p.733.
[5] H.Harada, T.Yamagata, S.Nakazawa, K.Ohno, and M.Yamazaki: Proc.of a Conference, "High Temperature Materials for Power Engineering 1990", held in Liege, Belgium, p.1319.
[6] D.D.Pearson, F.D.Lemkey and B.H.Kear:"Superalloys 1980", Proc.of 4th International Symposium on Superalloys, Seven Springs(1980)p.513.
[7] A.D.Cetal and D.N.Duhl: "Superalloys 1988", Proc. of the 6th International Symposium on Superalloys, Seven Springs(1988), p.235.
[8] D.J.Frasier, J.R.Whetstone, K.Harris, G.L.ErIckson and R.E.Schwer:Proc.of a Conference, "High Temperature Materials for Power Engineering 1990", held in Liege, Belgium, p.1281.
[9] D.Blavette, P.Caron and T.Khan: "Superalloys 1988", Proc. of the 6th International Symposium on Superalloys, Seven Springs(1988), p.305.
[10]K.Matsugi. R.Yokoyama, Y.Murata, M.Morinaga and N.Yukawa: Proc. of a Conference, "High Temperature Materisls for Power Engineering 1990", held in Liege, Belgium, p.1251




