[HOME]
Y. Yamabe-Mitarai and H. Harada
High Temperature Materials 21 Project
National Institute for Materials Science (NIMS)
1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
The alloys with the fcc and L12 two-phase coherent structure based on platinum group metals, mainly Ir have been developed as high-temperature materials. It was found that binary Ir-based alloys showed high strength up to 1200 °C, however the strength above 1200°C decreased drastically. Furthermore, binary alloys were very brittle. To ovsercome these problems, third or forth elements were added to binary alloys. The strength of binary, ternary and quaternary alloys is discussed in terms of the lattice misfit and precipitate morphology. Creep properties of these alloys were also investigated. Ni and Zr were effective elements for improvement of creep life at 1650 and 1800 °C.
Keywords: 0.2% flow stress, creep, Larson-Miller parameter, coherent structure, high-temperautre materials
To develop new generation high-temperature materials, we have developed fcc and L12 two-phase alloys using platinum group metals as base materials [1,2]. One of the authors and his co-workers have shown that the fcc and L12 two-phase coherent structure plays important role in strengthening the alloy at high temperature because the coherent interface between the matrix and the precipitates inhibits dislocation movement in well known Ni-based superalloys [3-5]. We considered that if the melting temperature of the base metal is higher than Ni and the alloy also has the fcc and L12 coherent two-phase structure similar to Ni-based superalloys, the alloys can be expected to have high strength at higher temperatures where Ni-based superalloys can not be used. Platinum group metals were investigated because of the fcc structure, good oxidation resistance and stability in chemical environments. Among the platinum group metals, Ir and Rh were chosen. The melting temperatures of Ir and Rh are high, 2447 and 1960°C, respectively. The Young's moduli at room temperature are also very high, 570GPa for Ir and 384GPa for Rh, respectively [6]. The strength of Ir at 1200 °C is the second-highest elevated-temperature strength among metal-based materials, next to that of W [7]. It is also known as the most stable element for corrosion [8]. On the other hand, the disadvantages of Ir are high density (22.7 g/cm3), brittleness unlike typical fcc metals, and limited supply, 4 tons/year in the world, resulting a high price. Rh is more ductile than Ir, although it still fails in an intergranular fracture mode. The density of Rh is almost half of Ir, about 12.4 g/cm3. The supply is higher than Ir, at 15 tons/year. However the price is three or four times higher than Ir.
During the past few decades, platinum group metals have been noted as high temperature materials. For example, the Ir-0.3%W alloy (fcc single-phase) containing Th below 60 ppm (designated at DOP-26) is currently used as a fuel-cladding material in radioisotope thermoelectric generators, the major source of onboard electric power in interplanetary spacecraft [for example, 9]. Several intermetallics have also been investigated, for example, IrNb with an L10 structure [10], RuAl [11], RuTa [12], and IrAl [13, 14] with a B2 structure. While these research projects concentrated on single-phase alloys, we have examined the fcc and L12 two-phase alloys. We have designated alloys with the fcc and L12 two-phase coherent structure using Ir or Rh as "refractory superalloys" and have focused on investigating Ir-based alloys. Similar trials have been performed for Pt-alloys. Among these are Pt-Zr and Pt-Hf systems where the fcc and L12 (Pt4Zr or Pt4Hf type L12) two-phase structure was found by systematic phase constituent studies [15, 16]. Addition of Rh for the Pt-Zr and Pt-Hf alloys also resulted in the fcc and L12 two-phase region in these ternary systems. Additional trials have been performed for the Pt-Al system. The L12-Pt3Al become stable from low temperature to high temperature by the addition of third elements such as Ti, Ta, and Cr although Pt3Al changes from L12 phase to D024 phase below 1260°C in Pt-rich region in Pt-Al binary system [17-19]. Thus the fcc and L12 two-phase region was also found in the Pt-Al-X (X = Ti, Ta, and Cr) systems.
In the present paper, the high-temperature strength and the creep behavior of the Ir-based alloys that have been developed in the "High Temperature Materials 21 Project" are described in terms of the precipitate morphology and the lattice misfit between the fcc matrix and the L12 precipitates. The target temperature capability for these alloys is 1000 hours creep life at 1800°C and a stress of 137MPa. Some of the alloys developed were demonstrated 1679°C of temperature capability at 137 MPa. From this point of view, the potential of Ir-based alloys as high-temperature materials is discussed.
According to binary phase diagrams [20], the fcc and L12 two-phase region exists in binaries of Ir and Nb, Ta, Ti, U, V, Hf, and Zr, and binaries of Rh and Am, Ce, Hf, Nb, Np, Ta, Th, Ti, Zr, V, and U. Among them, Nb, Ta, Ti, V, Hf, and Zr were chosen for second element additions for Ir. Nb, Ta, and Ti were chosen for second element additions for Rh alloys. A two-phase structure was observed in all binary systems. The coherency between the phases was also confirmed for the Ir-Nb, Ir-Ta, Ir-Hf and Ir-Zr alloys [2, 21]. Some of the Ir-based binary alloys showed superior strengths up to 1200°C, however the strength above 1200°C was not remarkable considering the high melting temperature [22]. The strength of Rh-based binary alloys were almost half of those of Ir-based binary alloys when the alloys with same second element were compared each other (for example, comparison of Ir-Nb and Rh-Nb) [23]. We also found that Ir-based binary alloys failed mostly by intergranular fracture similar to pure Ir [24]. Another disadvantage of Ir-based alloys is that their density is high about 20 g/cm3.
To solve these problems, ternary and quaternary additions have been investigated. In the Ir-Nb binary, cuboidal L12 precipitates similar to Ni-based superalloys were found, so Ir-Nb alloy was chosen as a base material. Ternary addition of Ni, Al, Zr, Mo, B, C were chosen. Ni was chosen because Ni is fully miscible with Ir in the Ir-Ni binary system and the fcc and L12 two-phase region is expected to remain over a wide range of composition. A density decrease is also expected because the density of Ni (8.5g/cm3) is less than half of Ir (22.5 g/cm3). Al is expected as solid solution hardening element because the atomic size of Al is larger than Ir. Zr is L12 forming element and the Ir-Zr alloy with the fcc and L12 two-phase showed higher strength than Ir-Nb alloys in the previous study [21]. We expected to improve strength of the Ir-Nb alloy by addition of Zr. Mo was added because its melting temperature is high (2630°C) and Mo is often added as a solid-solution hardening element in Ni-based superalloys. Boron improves grain boundary strength in Ni-based superalloys [for example 25]. Carbon is added as a stabilizer for the grain boundaries in Ni-based superalloys [for example 26]. For these reasons B and C might be expected to improve grain boundary strength of Ir-based alloys.
An additional set of trials focused on the combination of the two-phase Ir-Nb and Ni-Al alloys. When both binary systems have the fcc and L12 two-phase region, it is expected that the fcc and L12 two phase region is connected from Ni-Al side to Ir-Nb side in quaternary alloys. The quaternary alloys can be expected to have the advantages of both systems, that is, high strength at high temperature from the Ir-Nb and good ductility and low density from the Ni-Al. Furthermore, solid solution strengthening can be expected at higher temperatures above 1200°C. It is also possible to control strength, ductility, and density by control of alloy composition. From a different point of view, this alloy can also be called an Ir-Ni-based alloys containing some fcc or L12-phase former elements.
Among the above trials, the effect of addition of Ni, Al, Zr, Ni+Al on the lattice misfit, resulting precipitate morphology change, strength, and creep properties are shown in this paper. Strength behavior, ductility, and fracture mode of ternary alloys containing other elements and quaternary additions have been investigated by Gu and Yu [27, 28].
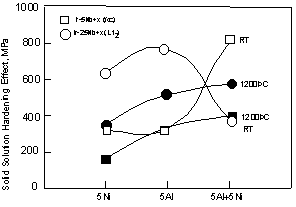
The lattice parameter of the Ir-based alloys was measured at room temperature using heat-treated bulk sample by X-ray diffractometry. The lattice parameter changes caused by additions of 5at%Ni, 5at%Al, and 5at%Ni+5at%Al to the Ir-5at%Nb alloy with the fcc single-phase and the Ir-25at%Nb alloy with the L12 single-phase are shown in Fig. 1. Here pure Ir, Ir-2at%Nb with the fcc single-phase, and Ir-25at%Nb (Ir3Nb) with the L12 single-phase are also shown for reference because we did not have the lattice parameter data for Ir-5at%Nb . For the fcc phases, the addition of Nb at least up to 2at% to pure Ir does not affect the lattice parameter. By further addition of Ni to the Ir-Nb alloys, the lattice parameters of both of the fcc and L12 phases increased slightly. Goldschmidt's atomic radii of these respective elements are shown in Table 1. The atomic radius of Ni is smaller than Ir and Nb. In spite of this, the lattice parameter
| Element | Goldschmidt's atomic radius, nm | Relative atomic radius for Ir |
| Ir | 0.135 | 1 |
| Nb | 0.147 | 1.09 |
| Ni | 0.125 | 0.93 |
| Al | 0.143 | 1.06 |
| Zr | 0.16 | 1.19 |
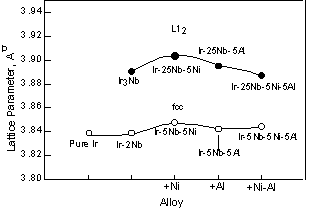
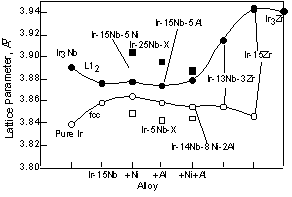
increased by addition of Ni. On the other hand, the addition of Al increased the lattice parameter, but this increase was less than that caused by the addition of Ni, although the Al radius is larger than that of Ir. When Ni and Al were added to the Ir-Nb alloys, the lattice parameter of the fcc phase was almost equivalent to that of the Ir-5at%Nb-5at%Al. On the other hand, the lattice parameter of the L12 phase with both Ni and Al became smaller than that of Ir3Nb +5at%Al. It is likely that this difference is caused by site occupation differences in each phase, although we do not have any data on this specific aspect of these alloys. However, when these elements were added to two-phase alloys, the lattice parameter changed in deferent way. Figure 2 compares the lattice parameter of the fcc and L12 phases in two-phase alloys with those in the single-phase (square) alloys shown in fig. 1 for reference. The lattice parameter of two-phase alloys was investigated using constrained two-phase alloys. Each peaks from the fcc or L12 phases were clearly detected and the lattice parameter was estimated from each peak between 40 and 120 degree. Then the lattice parameters from each peak were plotted as a function of cos2? and determined by least squares refinements. Although the microstructure of the two-phase alloys will be explained in detail later in fig. 11 and 12, the coherent structure was observed in the Ir-Nb alloys. On the other hand, both of the coherent and semi-coherent structures were observed in the Ir-Zr alloys. This means that the lattice parameter of the Ir-Zr alloy is average of that in the coherent and semi-coherent structures. In the Ir-15at%Nb, the lattice parameter of the fcc phase increased from that of pure Ir (Fig. 2). On the other hand, the lattice parameter of the L12 phase decreased from that of Ir3Nb. Thus the difference of the lattice parameters of the fcc matrix and the L12 precipitates becomes smaller than that between pure Ir and Ir3Nb. This is because the large lattice of the L12 phase is compressed by the small lattice of the fcc phase and the small lattice of fcc phase is expanded by the large lattice of the L12 phase in two-phase alloys as shown in Ni-based superalloys [29]. Thus the L12 lattice become smaller than in single phase and the fcc lattice become larger than in single fcc phase. By addition of Ni, Al, and Ni+Al, the lattice parameter of the fcc and L12 phases was almost equivalent to that of those binary alloys. Compared with two-phase alloys and single-phase alloys, the fcc phase lattice parameter in two-phase alloys was larger than in single-fcc phase and the L12 lattice parameter in two-phase alloy was smaller than in the single L12 phase. The difference of the lattice parameter of the fcc and L12 phases becomes larger in order of Ni, Al and Ni+Al containing alloys. We showed the results of the Ir-14Nb-8Ni-2Al alloy instead of the results of the Ir-15Nb-5Al-5Ni alloy. Although the amount of Ni and Al is not 5at%, we think the composition difference is not so effective to see the lattice parameter change by addition of Ni and Al. On the other hand, the addition of Zr in the Ir-Nb alloy changed the lattice parameter of the L12 phase greatly. This is because the lattice parameter of Ir3Zr is large compared with the Ir3Nb.
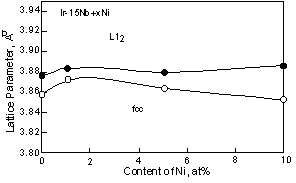
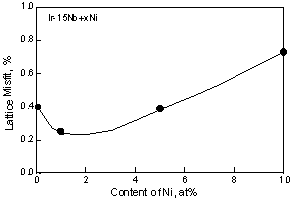
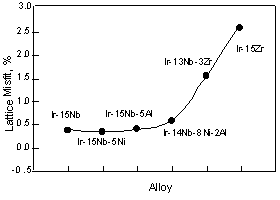
For Ni containing two-phase alloys, the influence of the Ni on the lattice parameter is shown in Fig. 3. The lattice parameter of the L12 phase slightly increased by addition of the Ni, however these were almost equivalent with increasing Ni. This is because Ni partitions into the Ir3Nb only a minor amount compared to the fcc phase. According to the ternary phase diagram, Ni partitions into Ir3Nb up to 5 or 6 at%. While Ni partitions to the fcc phase up to 45at% in the fcc + L12 two-phase alloy [30]. By addition of 1at%Ni, although the lattice parameter of the fcc phase increased slightly, with increasing Ni beyond this, the lattice parameter decreased. At the moment, it is not clear the reason why the lattice parameter of the fcc phase increased with the addition of 1at%Ni. The decrease of the lattice parameter of the fcc phase caused large differences between the lattice parameters of two-phases. Thus the lattice misfit, (ap-am)/a, where ap and am are the lattice parameter of the L12 precipitates and fcc matrix, of the Ni containing alloy increased with increasing Ni contents (Fig. 4). For the Al containing alloy, the Al prefers to partition into the fcc phase rather than the L12 phase [31]. However in two-phase alloy, the lattice parameters of the fcc and L12 phases are almost equivalent to that of binary alloy. This suggests that there is no clear effect of Al additions on the lattice parameter within the composition range investigated.
The lattice misfit between the two phases, (ap-am)/am, of alloys is shown in Fig. 5. The Ir-Nb binary, Ni and Al containing alloys showed similar lattice misfits. By addition of both of Ni and Al, the lattice misfit increased slightly. The addition of Zr resulted in a drastic increase of the lattice misfit.
Temperature dependence of the lattice misfit up to 1200 °C was measured for only binary alloys [32]. The lattice misfit was almost equivalent through testing temperature because the lattice parameter of the fcc phase increased as well as that of the Ll2 phase with increasing temperature.
The temperature dependence of the some of the Ir-based alloys is shown in Fig. 6. These alloys were prepared by arc melting method in an argon atmosphere and cylindrical samples 3 mm in diameter and 6
| Alloy composition, at% | Phase structure | Heat treatment, hours |
Test condition LM: lattice misfit |
| Ir-2Nb | fcc | 1200°C 100h | LM |
| Ir-10Nb | fcc | As cast | strength |
| Ir-15Nb | fcc+L12 | 1200°C 168h, 1200°C 72h | LM, strength |
| Ir-17Nb | fcc+L12 | 1800°C 24h | strength, Creep |
| Ir-25Nb | L12 | 2000°C 72h | strength |
| Ir-12Zr | fcc+L12 | 1200°C 10h, 1200°C 168h | Strength, Creep |
| Ir-15Zr | fcc+L12 | 1200°C 168h | LM |
| Ir-5Nb-5Ni | fcc | 1800°C 72h | LM, strength |
| Ir-15Nb-1Ni | fcc+L12 | 1800°C 72h | LM, creep |
| Ir-15Nb-5Ni | fcc+L12 | 1800°C 72h | LM, strength, creep |
| Ir-15Nb-10Ni | fcc+L12 | 1800°C 72h | LM, creep |
| Ir-25Nb-5Ni | L12 | 1800°C 72h | LM, strength |
| Ir-5Nb-5Al | fcc | 1200°C 150h | LM, strength |
| Ir-15Nb-5Al | fcc+L12 | 1200°C 150h | LM, strength |
| Ir-25Nb-5Al | L12 | 1200°C 150h | LM, strength |
| Ir-5Nb-5Ni-5Al | fcc | 1200°C 150h | LM, strength |
| Ir-14Nb-8Ni-2Al | fcc+L12 | 1500°C 24h | LM, strength |
| Ir-25Nb-5Ni-5Al | L12 | 1200°C 150h | LM, strength |
| Ir-13Nb-3Zr | fcc+L12 | 1500°C 72h | LM, strength, creep |
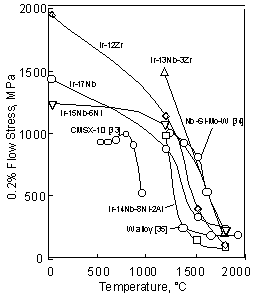
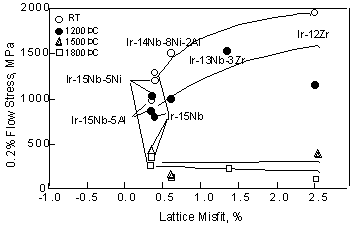
of Ir-based alloys with other high temperature materials. mm in height were cut from the alloy ingot. Then the cylindrical samples were heated in the two-phase region directly because the application of solution heat treatment in the fcc single phase in Ir-based alloys is difficult according to the phase diagrams [20]. The alloy compositions and heat treatments are shown in detail in Table 2. Heat treatment conditions were determined for each alloy to obtain homogenous structure or precipitation. The strengths of most of Ir-based alloys were above 1000MPa up to 1200 °C, (Fig. 6). On the other hand, the strength of the third generation Ni-based single crystal superalloys, such as CMSX-10, decreased drastically above 800°C [33]. However at 1500 °C, the strengths of the Ir-based alloys decreased drastically and were below 400MPa. At 1800 °C, the difference of the strength becomes smaller among the Ir-based alloys. This suggests that the ternary and quaternary were not effective in improving strength above 1500 °C. Compared with the Nb-based alloy [34], the strengths of the Ir-based alloys were not remarkable. The strength of the Ir-based alloys is plotted as function of the lattice misfit in Fig. 7. Here, the volume fraction of the Ir-15Nb and Ir-12Zr alloys was about 33 and 50%, respectively, according to phase diagrams [20]. Although the volume fraction of the Ir-Nb and Ir-Zr alloys is different, the strength of the Ir-Nb alloy with 50% L12 phase was as same as that of Ir-15Nb alloy. Here to compare with ternary and quaternary alloys, the strength of the Ir-15Nb is shown. Ir is difficult to investigate the volume fraction of ternary and quaternay alloys because of their fine precipitates. However, we consider that there is no large difference of the volume fraction by addition of small amount of elements. Below 1200°C, strength increased with increasing the lattice misfit, although the strength of the Ir-Zr binary alloy with 2.5% lattice misfit is lower than that of the Ir-Nb-Zr alloy with 1.5% lattice misfit. Among the alloys with about 0.4% lattice misfit, strengths of them were varied. Above 1500°C, there is no relationship between strength and the lattice misfit and only small difference among the alloys was found. These results shows that the lattice misfit is effective for the strength below 1200°C, however at high temperature, the lattice misfit effect is not great.
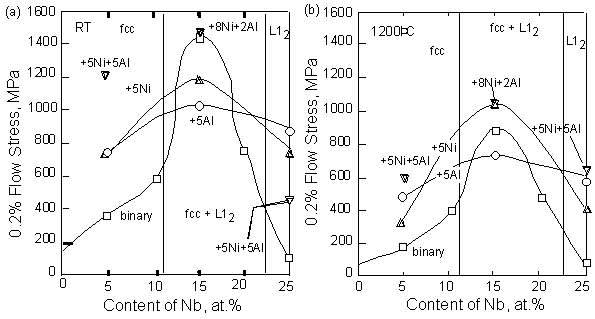
The compressive strength as a function of Nb content is shown in Fig. 8. In binary Ir-Nb alloy, the increase of the strength by addition of Nb shows solid solution effect of Nb in the fcc phase. The strength increased by addition of Ni, Al and Ni+Al from the strength of binary alloy. This shows additional solid solution hardening effect by these elements. In the L12 phase, solid solution hardening effects by addition of these elements were also observed as well as in the fcc phase. To clarify the solid solution effect by each element, the difference between the strength of the single-phase ternary and quaternary alloys and single-phase binary alloy (Ir-5Nb or Ir-25Nb) is shown in each alloys in Fig. 9. The grain size of ternary and quaternary alloys were almost equivalent each other, however it was valid between a few hundred ?m and a few mm within each samples. The grain size of binary alloys was a few hundred ?m in the Ir-10Nb alloy and about 50 ?m in Ir-25Nb alloy. Although the grain size became larger with the addition of these elements, the strength was higher in ternary and quaternary alloys compared to the binary alloy. This suggests that the solid-solution effect of Ni and Al is very large enough to overcome the grain size effect. The solid-solution hardening effect for both of the fcc single-phase and L12 single-phase increased in order of the Ni containing alloy, the Al containing alloy and the Ni+Al containing alloy at 1200 °C. At room temperature, although the strength of the fcc-alloy including Ni+Al is low, the Al effect was larger than the Ni effect in the fcc?alloy. For the L1 single-phase, the effect of Ni and Al was almost equivalent. Considering the lattice parameter of these single phase alloys (Fig. 1), Ni was the element which changed the lattice parameter of both of the fcc and L12 phases drastically. Thus it is considered that the distortion of lattice is largest in the Ni containing alloy. In spite of this, the solid-solution effect was smallest. The reason is not clear.
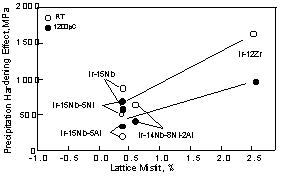
In addition to solid-solution hardening effect, the further increase of the strength in two-phase alloys due to a precipitation-hardening effect is clear in these alloys (Fig. 8). The precipitation hardening effect is estimated from the difference between the experimental data and the strength estimated by role of mixtures of law only for independent deforming phases from the strength of the single fcc and L12 phases. For binary alloys, the strength of the 10Nb alloy (which compositions close to equilibrium composition) is used as the strength of the fcc phase. The strength of the L12 is taken as the alloy with 25Nb alloy, although this is not the equilibrium composition in the binary system. For other alloys, it is difficult to determine tie lines because of fine-scale microstructure. In this case, the strength of 5at%X (X=Ni, Al or Ni-Al) containing Ir-5Nb and Ir-25Nb alloy, and two-phase alloy was compared. Furthermore, we did not have data of Ir-15Nb-5Ni-5Al alloy, so we used the strength of Ir-14Nb-8Ni-2Al in Fig. 8. These precipitation hardening effects are also plotted as a function of lattice misfit in Fig. 10. The open and solid symbols represent room temperature and 1200 °C, respectively. Among the alloys with similar lattice misfit, the Ir-Nb binary alloys showed a greater degree of precipitation hardening, compared to the ternary and quaternary alloys. Additions of Ni, Al and Ni+Al were not effective for precipitation hardening. Among these alloys, Al was less effective element at both testing temperature. The precipitation hardening of the Ir-Zr alloy compared with the fcc phase including Zr and the Ir3Zr are also plotted in Fig. 10. The Ir-Zr alloy with large lattice misfit showed largest precipitation hardening.
The deformation modes observed for the Ir-based alloys for compressive test with strain rate 10-4 /s after a few % deformation below 1200 °C are summarized in Table 3. Only Ir-Nb alloy showed a bypass mode [22]. Other alloys deformed by the precipitate shearing mode [36-39]. Binary alloys showed highest precipitation ?hardening effect among Ir-Nb-based alloys. When deformation occurs by shearing mode, precipitation hardening is controlled by precipitate morphology, interface resistance determined by coherency or misfit dislocations, and the strength of the L12 phase. The precipitate morphology was slightly
| Alloy | Lattice misfit, % | Deformation mode |
| Ir-15Nb | 0.4 | Bypass |
| Ir-15Nb-5Ni | 0.4 | Shearing |
| Ir-15Nb-5Al | 0.4 | ? |
| Ir-14Nb-8Ni-2Al | 0.6 | Shearing |
| Ir-12Zr | 2.6 | Shearing |
different among the alloys (Fig. 11). A cuboidal shape was more clear in the Ir-Nb-Ni-Al alloy. In the Ir-Nb-Ni alloy, the edges of cuboidal precipitates assume more spherical shape. Despite of this difference of precipitate morphology, the degree of precipitation hardening among these alloys was almost equivalent. This suggests that precipitate morphology does not contribute to precipitation hardening. Considering interface resistance, interface resistance is governed by coherency strain or misfit dislocations. It is considered that when the lattice misfit is equivalent, coherency strain energy is also equivalent. From this point, coherency strain seems to be equivalent among these alloys because of similar lattice misfit. Although we observed misfit dislocations in only the Ir-Nb-Ni alloy, this is not effective because the precipitation hardening effect is not as large in the Ir-Nb-Ni alloy compared with other alloys. Considering the strength of the L12 phase, as shown in Fig. 9, the addition of Ni+Al is most effective in strengthening the L12 phase. Furthermore we found the fcc phase in the L12 phase in the Ir-Nb-Ni-Al alloy. This suggests that a dislocation will meet more interfaces in the Ir-Nb-Ni-Al than in other alloys because of t existence of the interface in the L12 phase. However, these factors are not effective for precipitation hardening. based on the investigations to date, it is not yet clear which factor is more effective for precipitation hardening effect when deformation occurs in the shearing mode. On the other hand, only the binary Ir-Nb alloy deformed by bypass mode. This alloy showed highest degree of precipitation hardening. The reason why only the Ir-Nb alloy deformed in the bypass mode is not clear as the precipitate size and shape of Ir-Nb binary alloy are similar to other alloys. It will be difficult to bypass in the fcc phase in ternary and quaternary alloys, because the solid-solution effect was very large in these alloys. If binary Ir-Nb alloy also deforms by shearing mode, it is considered that precipitation-hardening effect is equivalent to other alloys. We can say that by some reason, the precipitation-hardening was larger in the alloy deformed by bypass mode than in the alloy deformed by shearing mode.

Precipitate morphology changed drastically when the lattice misfit increased to 2.5% in the Ir-Zr alloy (Fig. 12). Plate-like precipitates formed and these precipitates formed a three dimensional maze structure. The structure is semi-coherent structure with a high density of misfit dislocations formed at the interface. Below 1200°C, the strength of the Ir-Zr two-phase alloy was higher than that of the Ir-Nb two-phase alloy (Fig. 6). Here, the volume fraction of the L12 precipitates is 50 % in both alloys. As shown in the previous session, both solid-solution hardening and precipitation-hardening were observed in the Ir-Nb alloy. Both hardening effects were also observed in the Ir-Zr alloy [40]. The precipitation-hardening was larger in the Ir-Zr alloy than in the Ir-Nb alloy. The deformation mode was shearing in the Ir-Zr alloy [21]. In this case, the precipitate morphology effect is very clear. When a dislocation moves through fcc matrix, it will frequently encounter interfaces in the maze structure of the Ir-Zr alloy. The coherent interface has high coherency strain energy in the maze structure and a high density of misfit dislocations may prevent movement of dislocations in the semi-coherent structure. This is attribute to a high degree of precipitation hardening in the Ir-Zr alloy. However, above 1200°C, precipitation hardening effect was minor. Deformation structure in the deformed sample with a few % at 1800°C showed many dislocations within precipitates in the Ir-Zr alloys with the coherent or semi-coherent interfaces no longer servivs as obstacles for dislocations [21]. In the Ir-Nb alloys, a precipitate shape change was observed at 1800°C. This shows that not only the matrix but also the precipitates deform at high temperature. For other Ir-Nb based alloys, similar phenomena occur, though deformation structure have not yet been chracterized.

Compressive creep curves are shown for Ir-Nb, Ir-Zr, Ir-Nb-Ni and Ir-Nb-Zr alloys at 1500, 1650, and 1800°C under 137MPa in fig. 13. At 1500°C, the creep strains of the binary alloys were below 2% after 300 hours. The creep resistance of the Ir-Nb alloy is higher than that of the Ir-Zr alloy. This is because the maze structure was coarsened by discontinuous coarsening from grain boundary in the Ir-Zr alloy. When the coherency strain energy of the interface is very high in the alloy with large lattice misfit, coarsening also easily occurs with a high degree of misfit. However since it is considered that coarsening of the maze structure itself is difficult due to slow diffusion at coherent boundary, discontinuous coarsening occurred. Similar coarsening is observed in the lamellar structure. When the lamellae are very fine, coarsening often occurs by migration of grain boundary [41]. At 1650°C, tertiary creep was clearly observed in the Ir-Nb binary alloy. On the other hand, creep properties were improved by addition of Ni. The creep strain of the Ir-Nb-Ni alloy was below 2% after 300 hours. No tertiary creep was observed in compression. At 1800°C, binary alloys showed clearly tertiary creep and they failed after only a few hours. However with the addition of Zr, the creep life was improved drastically. Creep strain was reduced to approximately 2% after 100 hours. No tertiary creep was observed. for comparison a Ni-based superalloy, TMS 75, had a rupture life of 196 hours under 98MPa in a tensile condition at 1150°C [42]. However, under compression stress at 1200°C, the sample was buckled, and creep strains could not be accurately measured. Another comparison test indicated that the compressive creep strain rates of an IrAl single-phase with a B2 structure at 1100°C were between 10-6 and 10-5 s-1 under between 100 and 220 MPa [43]. The strain rate of IrAl at 1100°C was one or two orders higher than that of the Ir-based alloys (10-7 s-1) at 1500°C. This demonstrates that these alloys with fcc and L12 two phase are more promising materials in terms of their creep resistance. The Larson-Miller parameter P calculated for these alloys using 1% strain, (P=T(log t +20), T [K], t[h]), were between 39000 and 45000. The capability temperature in which the creep life is 1000 hours was calculated from the Larson-Miller parameter. The capability temperature of the Ir-Nb, Ir-Nb-Ni, and Ir-Nb-Zr alloys were 1452°C, 1543°C, and 1679°C, respectively. This shows that the capability temperature improved drastically, about 100°C by addition of Ni and 220°C by addition of Zr.
Deformation modes during creep are presently under investigation, so the mechanism by which Ni or Zr additions improve creep is not yet understood. The lattice misfit of Ir-Nb-Ni and Ir-Nb is similar, so the lattice misfit does not account for the creep properties. SEM observations of creep-induced damage showed many cracks around grain boundaries in the binary alloys. On the other hand, Ni-containing alloy did not have cracks. This suggests that Ni is effective to improve resistance to grain boundary sliding. We think similar phenomena also happened in Ir-Nb-Zr alloy.
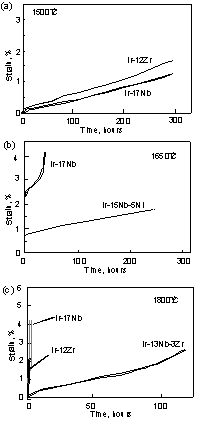
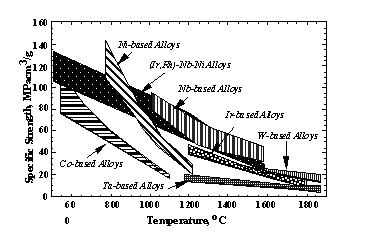
Table 4 summarizes mechanical properties, phase constitutets, density, and melting temperature of some of the Ir-based alloys. It is difficult to conclude which element is most suitable for improvement of properties of Ir-based alloys as high temperature materials. However the Ni, Zr and Ni+Al addition showed high strength and high melting temperatures if the amount of these additions is well controlled. The additions of Ni and Zr was particularly beneficial to creep properties. This is very promising as a basis for a high temperature material sytem. The specific strengths of Ir-based binary alloys are low because of their large density, as shown in Fig. 14. However when we replace Ir with Rh partially, the density can be decreased, maintaining high strength at high temperature [44]. Thus through a wide temperature region, Ir-Rh based alloys showed very high specific strengths.
We thank Dr. Y. F. Gu and Ms. C. Huang in NIMS for part of this work. We also thank Dr. X. H. Yu from Manitova University, who did part of this work during her stay at NIMS. We also thank Mr. S. Nishikawa and Mr. T. Maruko in Furuya Metal Co., Ltd. for supporting Ir.
| Alloys at% | Strength, MPa at 1200 °C | Strain, % | Temperature capability for 1000 hours, °C | Fracture mode | Phase | Density g/cm3 | Melting Temp. °C |
| Ir-15Nb | 800 | 7 | 1452 | Intergranular mode | fcc+L12 | 20.2 | 2400 |
| Ir-15Nb-10Ni | 800 | 7 | 1543 | Transgranular mode | fcc+L12 | 18.7 | >2000 |
| Ir-15Nb-5Mo | 800 | 5 | ? | Intergranular mode | fcc+L12 | 20 | >2000 |
| Ir-15Nb-500 ppmB | 500 | 5 | ? | Transgranular mode | fcc+L12 | 20 | >1300 |
| Ir-15Nb-500 ppmC | 1200 | 5 | ? | Transgranular mode | fcc+L12 | 20 | >2000 |
|
Ir-15Nb:Ni-19Al
=90:10 Ir-13.5Nb-8.1Ni-1.9Al | 1000 | 20 | ? | Transgranular mode | fcc+ Ir3Nb | 18.7 | >2200 |
|
Ir-20Nb:Ni-17Al
=50:50 Ir-10Nb-41.6Ni-8.4Al | 200 | 20 > | ? | Transgranular mode | fcc+ Ir3Nb+ Ni3Al | 14.8 | about 1700 |
| Ir-2.2Nb-76.9Ni-10Al | 50 | 20 > | ? | Transgranular mode | fcc+ Ni3Al | 8.9 | about 1500 |
| Ir-12.5Nb-3Zr | 1500 | - | 1679 | ? | fcc+L12 | 19.6 | >2200 |
| Ir-12Zr | 1900 | 7 | ? | fcc+L12 | 19.6 | 2100 |
[1] Y. Yamabe, Y. Koizumi, H. Murakami, Y. Ro, T. Maruko, and H. Harada, Scripta Mater., 35, 2, (1996), 211.
[2] Y. Yamabe-Mitarai, Y. Ro, T. Maruko, and H. Harada, Metall. Mater. Trans. A, 29A, (1998), 537.
[3] Y. Ro, Y. Koizumi, H. Harada, Mater. Sci. Eng. A, A223, (1997), 59.
[4] H. Harada, M. Yamazaki, Y. Koizumi, Tetsu to Hagane (in Japanese) 65, (1979), 1049.
[5] H. Harada, M. Yamazaki, Y. Koizumi, N. Sakuma, N. Furuya, H. Kamiya, Proc. of a Conference on High Temperature Alloys for Gas Turbines 1982, Liege, Belgium, 4- Oct 1982, D. Reidel Publishing Company, 1982, p. 721.
[6] International Tables of Selected Constants, 16, Metals,Thermal and Mechanical Data
[7] B. L. Mordike and C. A. Brookes, Platinum Metals Review, 4, (1960), 94.
[8] Metals Handbook, vol.2, 9th edition (ASM, Metals Park, OH, 1979).
[9] C. T. Liu, H. Inouye, and A. C. Schaffhauser, Met. Trans. A, 12A, (1981), 993.
[10] R. L. Fleicsher, R. D. Field, K. K. Denke, and R. J. Zabala, Met. Trans. A, 21A, (1990), 3063.
[11] R. L. Fleicsher and R. D. Field, and C. J. Briant, met. Trans. A, 22A, (1991), 403.
[12] R. L. Fleicsher, R. D. Field, C. L. Briant, Met. Trans. A, 21A, (1991), 129.
[13]P. J. Hill, L. A. Cornish, and M. J. Witcomb, J. of Alloys and Compounds, 280, (1998), 240.
[14] H. Hosoda, T. Takasugi, M. Takehara, T. Kingetsu, and H. Masumoto, Mat. Trans. JIM, 38, 10, (1997), 871.
[15] G. B. Fairbank, C. J. Humphreys, A. Kelly, C. N Jones, Intermetallics, 8, (2000), 1091.
[16] G. B. Fairbank, C. J. Humphreys, A. Kelly, C. N Jones, Proc. of the 5th Inter. Charles Parsons Turbine Conf., 2000, p. CP-58.
[17] P. J. Hill, Y. Yamabe-Mitarai, and I. M. Wolff, Scripta Mater. 4, (2001), 43.
[18] P. J. Hill, Y. Yamabe-Mitarai, H. Murakami, L. A. Cornish, M. J. Witcomb, I. M. Wolff, and H. Harada, Proc of Structural Intermetallics 2001, 2001, acceppeted.
[19] P. J. Hill,T. Biggs, P. Elis, J. Hols, S. Taylor, and I. M. Wolff, Mat. Sci. Eng. A, 301, (2001), 167.
[20] "Binary Alloy Phase Diagrams", ed by T. B. Massalski, ASM, (1992).
[21] Y. Yamabe-Mitarai, Y. Ro, S. Nakazawa, T. Maruko, and H. Harada, Defect and Diffusion Forum, vols. 188-190, (2001), 171.
[22] Y. Yamabe-Mitarai, Yuefeng Gu, Y. Ro, S. Nakazawa, T. Maruko, H. Harada, Scripta Mater. 41, 3, (1999), 305
[23] Y. Yamabe-Mitarai, Y. Koizumi, H. Murakami, Y. Ro, and T. Maruko, and H. Harada, Scripta Materialia, 36, 4, (1997), 393.
[24] Yuefeng Gu, Y. Yamabe-Mitarai, Y. Ro, and H. Harada, Scripta Mater., 40, 11, (1999), 1313.
[25] J. Kameda and A. J. Bevolo, Acta Metall. Mater. 41, 2, (1993), 527.
[26] R. T. Holt and W. Wallace, International Metals Reviews, March, (1976), 1.
[27] Y. F. Gu, Y. Yamabe-Mitarai, Y. Ro, S. Nakazawa, and H. Harada, to be submitted to this issue.
[28] X. H. Yu, Y. Yamabe-Mitarai, Y. Ro, S. Nakazawa, and H. Harada, to be submitted to this issue.
[29] K. Ohno, K. Ohsumi, H. Harada, T. Yamagata, and M. Yamazaki, Adbances in X-ray Analysis, 34, (1991), 493.
[30] Yurfeng Gu, Y. Yamabe-Mitarai, Y. Ro, T. Yokokawa, and H. Harada, Scripta Materialia, 39, 6, (1998), 723.
[31] Seiji Miura, Kenji Ohkubo, Yoshisato Kimura, Yoshinao Mishima, Yoko Yamabe-Mitarai, Hiroshi Harada and Tetsuo Mohri : to be submitted to J. Phase Equilibria.
[32] Y. Yamabe-Mitarai, Y.Ro, T. Maruko, T. Yokokawa, and H. Harada, Proc of Structural Intermetallics 1997, eds. by M. V. Miracle, R. Wagner, and M. Yamaguchi, TMS, 1997, p.805.
[33] G. L. Elickson, Superalloys 1996, TMS, Warrendale, PA, 1996, p. 35.
[34] C. L. Ma, A. Kaasama, Y. Tan, H. Tanaka, R. Tanaka, Y. Mishima, and S. Hanada, Report of the 123rd Committee on Heat-Resisting Materials and Alloys, 40, 3, (1999), 349.
[35] W. F. Brown, Jr., H. Mindin, N. C. Ho, Aerospace structural Metals Handbook, CIDAS/Purdue University, Weat Latayette, IN, 5, 1992, 5502.
[36] Y. F. Gu, Y. Yamabe-Mitarai, Y. Ro, T. Yokokawa, and H. Harada, Metall. Mat. Trans. A, 30A, (1999), 2629.
[37] Y. Yamabe-Mitarai, Yuefeng Gu, Y. Ro, S. Nakazawa, T. Maruko, and H. Harada, Scripta materialia, 41, 3, (1999), 305
[38] X. H. Yu, Y. Yamabe-Mitarai, S. Nakazawa, Y. Ro, and H. Harada, Met Trans, 32A, (2001), 1347.
[39] X. H. Yu, Y. Yamabe-Mitarai, Y. Ro, and H. Harada, Key Engineering Materials, vols 171-174, (2000), 677.
[40] Y. Yamabe-Mitarai, Y. Ro, T. Maruko, and H. Harada, Intermetallics, 7, (1999), 49.
[41] J. D. Livingston, and J. W. Cahn, Acta Metall., 22, (1974), 495.
[42] Y. Koizumi, T. Kobayashi, T. Kimura, M. Osawa, and H. Harada, Proc. of Materials for Advanced Power engineering 1998, 1998, p. 1089.
[43] A. Chiba, T. Ono, X. G. Li, and S. Takahashi, Intermetallics, 6, (1998), 35.
[44] Y. F. Gu, Y. Yamabe-Mitarai, S. Nakazawa, Y. Ro, and H. Harada, Met Trans, accepted.