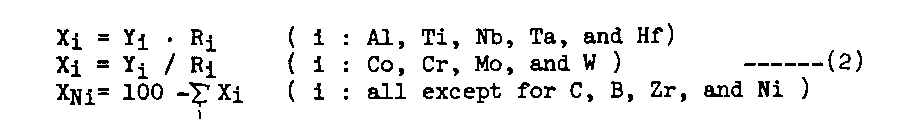Abstract

An alloy design system has been established for gamma-prime precipitation hardening nickel-base superalloys.
As the first part of our system, a calculation of component phases and predictions of properties of alloys were made possible with help of a regression analysis applied for the reported data.
Then approximately 100 alloys were designed through the system and evaluated by creep rupture tests, a tensile test, and a hot corrosion test. A number of alloys developed have creep rupture strength superior to that of commercial alloys(IN-738LC, B-1900Hf, Mar-M247, etc.) when comparison was made among those with a comparable hot corrosion resistance. Some of them showed good tensile properties as well.
Afterwards regression analyses were again applied over all the above properties of the alloys we designed and tested. It was found that the properties were well related to structural factors such as alloy composition, gamma-prime fraction, and gamma-prime composition. The resultant equations of analyses have been adopted to our alloy design to manufacture superior alloys.

1. Introduction

This paper reports our alloy design system which predicts compositions of nickel-base superalloys having desired quality for gas turbine, and actual superalloys which have been prepared through the alloy design system. Three fandamental factors, i.e. creep rupture strength, tensile properties, and hot corrosion resistance are selected as the key properties to be checked in our design system.

2. Outline of our alloy design system[l,2]

Flow chart of our design system is schematically summerized in Fig.l. Its details are as follows;
i) A regression analysis was applied over compositions of gamma-prime phase of 24 commercial or experimental alloys[3,4]. The resultant equation is shown in Table 1. This equation also contains the region where gamma-prime is considered to be unstable because of excessive solution. This area is eliminated by PHACOMP[5] and SI (Solubility index [6]) defined by eq.(1). The area of gamma-prime surface is depicted in Fig.2.

ii) The composition of the gamma phase equilibrated with a given gamma-prime phase lying on the gamma-prime surface is calculated by the partitioning ratios (Ri), which are determined by the composition of the gamma-prime phase through regression analyses (Table 2). The composition of gamma (Xi) is calculated by eq.s(2). PHACOMP[7] is again applied to eliminate unstable composition.

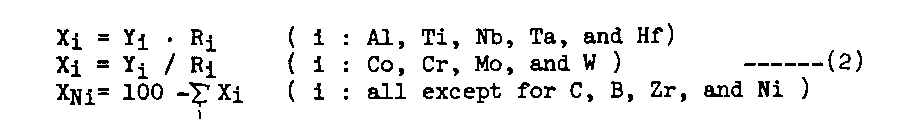
iii) Composition (C.) of a (gamma + gamma-prime) for a given gamma-prime fraction (f) is obtained by eq.(3) which is the equation of tie-line combining the compositions of gamm and gamma-prime in the state of equilibrium.

iv) When carbon and/or boron are added, amounts of each metals required for the carbides and/or borides are calculated to be equilibrated with the gamma and gamma-prime, and then added with carbon and boron. Regression analyses[4,5] were used to calculate fractions of various carbides and to calculate composition of MC carbide. ComPoSitions of M₂₃C₆, M₆C, M₃B₂, and M₅B₃[8] were assumed to be reasonable for the (gamma + gamma-prime) composition in the same manner as PHACOMP[5].
v) Melting points of alloys of the given composition are calculated through regression analyses (Table 3) derived from the data of pure Ni, Ni-X alloys (X= Co, Cr, Mo, W, Al, Ti, Nb, and Ta)[9], and 18 commercial cast alloys[10,11]. Creep rupture strength of alloys are calculated through regression analyses (Table 4) derived from the data of 21 commercial cast alloys[10]. Predictions of other properties shown in broken line frame in Fig.1 were made possible by quantitative analyses discribed in section 4.
Accoding to equations in Table 4, creep rupture strength is to increase with increase of gamma-primefraction, but it is unlikely that the creep rupture strength is the largest when an alloy is composed of gamma-prime alone. This implies that there would be a limit beyond which the equations are no longer valid. In order to check it, we prepared a series of alloys in which gamma-prime fraction varied from 0 vol% to 100 vol% while compositions of gamma and gamma-prime remain virtually constant.
The compositions of alloys were specified by the left hand side of eq.(3) substituting the gamma and gamma-prime compositions in Inconel 713C[3] and optional fractions of gamma-prime into right hand. Structures of these alloys are- shown in Fig.3.gamma-prime amounts experimentaly deter- mined for these alloys are shown in Fig.4. Compositions of individual phases analyzed by EPMA are substantially constant in the alloys. The resultant variation of creep rupture strength against gamma-prime fraction is shown in Fig.5. This shows that the experimental curve taper-off when gamma-prime fraction exceeds about 50 vol%, and even decreases beyond 62.5 or 75 vol%. From this fact it has been concluded that the gamma-prime fraction should be about 65 vol% to have the maximum precipitation hardening.

3. Alloy development[1,12,13]

With help of our alloy design system, approximately 100 alloys were designed, vacuum cast to size to specimen with about 1 -3 mm of grain size, and tested in terms of creep rupture strength, tensile properties, and hot corrosion resistance.
All the alloys were designed to be composed of highly solid solutioned gamma and gamma-prime phases (SI=1.3 to 1.4), and their content of solid solutioning elements, Cr, Ti, W, and Ta, were varied over a wide range with respect to three points as follows ; i) prediction of creep rupture strength by equations in Table 4, ii) effect of Cr on the hot corrosion resistance, and iii) effect of Ta on the high temperature strength. Fractions of gamma-prime in these alloys were usually designed to be 65 vol%. Compositions of typical successful alloys are shown in Table 5, and they are plotted in schematic phase diagram as shown in Fig.6
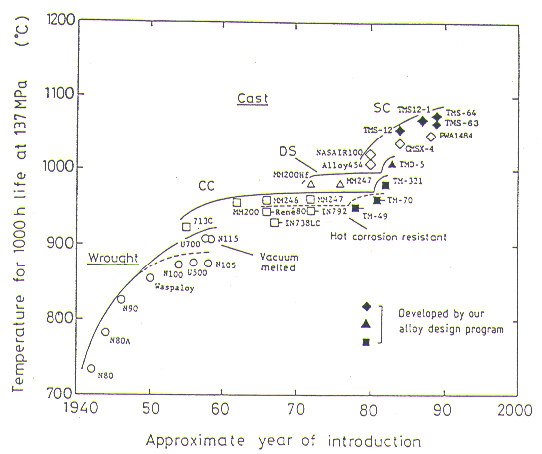
Fig.7 illustrates plots of creep rupture life against hot corrosion resistance for our typical successful alloys together with those of some representative commercial alloys. It should be noted here that our alloys have longer creep rupture life than the commercial ones when comparison is made among the alloys with a comparable hot corrosion resistance.
Out of these alloys, TM-49, TM-104, TM-70(TM-47Hf), TM-234, and TM-268 are considered to be prospective candidates for practical gas turbines since they have satisfactory elongation (8-12%) in high temperature tensile testing. These alloys are being tested at NRIM in terms of some other properties, which include diffusion and PVD (Physical vapour deposition) coatings[l4,15], effects of HIP and coatings on the low cycle fatigue[l6] and thermal fatigue [17], and so on. Castabilities of alloys TM-49, TM-104, TM-70, TM-114, TM-115, and TM-171 are satisfactory ; we have succeded in manufacturing thin (0.5 mm minimum) hollow blade of these alloys.
Single crystal alloys with superior quality can be obtained by our alloy design. Alloy TMS-2, strengthened by W and Ta, has a longer creep rupture life than NASAIR 100 (Mar-M247 modified for SC)[18] after a directional solidification and without further heat treatment, as shown in Fig.8. It is predicted through our regression analysis that the solidus temperature of TMS-2 is higher than NASAIR 100 by 60 deg.C.

4. Quantitative analysis of the properties

4.1. Creep rupture strength

It is well indicated in Fig.9 that the creep-rupture-life/ gamma-prime-fraction plots are different for each series of alloys but every series is likely to have a max~mum in the vicinity or more than 75 vol%. This means that the creep rupture life depends partly on solid solution hardening and partly on gamma-prime precipitation hardening. The latter effect should be approximated by an equation including a quadratic term or higher one. The regression analysis employing the quadratic term covering our 52 alloys of 50 to 80 vol% of gamma-prime gives the result shown in Table 6. From this equation it is understood that the maximum solid solution hardening is to be achieved when Cr in gamma-prime is substituted by W and Ta.
By differentiating the equation, the gamma-prime fraction is to be obtained for the maximum precipitation hardening, and the calculated value for it is 86 vol%. This value, however, seems to be a little too large when compared with the plot in Fig.9 and Fig.5. There are two reasons considered ; i) approximation with a quadratic term may not be good enough, ii) gamma-prime fraction in actual alloys at 1000 deg.C may be smaller than that designed. The latter has been certified in two series of alloys, a series containing TM-49 and that containing TM-47.

4.2. Tensile properties

Tensile properties at 900 deg.C were observed for the specimen solution treated in various conditions followed by an aging treatment. Fig.10 shows gamma-prime fraction dependance of three properties observed when the other factors were kept in the specified condition (Values for Mar-M247 are also included in the chart). Obviously the variations are well approximated with linear functions of gamma-prime fraction. Results obtained from other series of alloys have indicated that the linearities holds in the range of 50 to 80 vol% of gamma-prime fraction, which differ from the case of creep rupture strength.
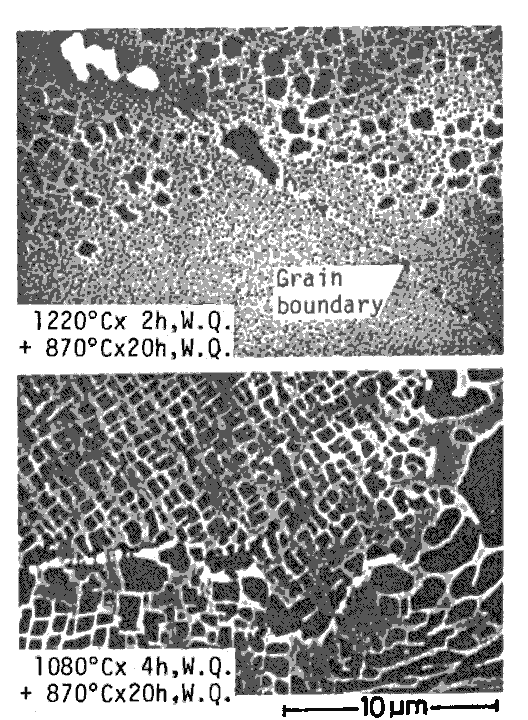
Effect of solution temperature is linear as well, although ultimate tensile strength is almost independent of it as shown in Fig.11. A higher solution temperature gives a higher yield strength. The lower the solution temperature is, the larger is the tensile elongation, but this tendency ceases to work below a certain temperature; solution treatment below 1080 deg.C gave no advantage effect on tensile elongation of three alloys developed.
The regression equations for tensile properties derived from the 46 sets of data for alloys of 50 to 80 vol% gamma-prime and solutioned at 1080 to 1220 deg.C are shown in Tables 7 and 8. Equations in Table 7 reveal that the yield strength and ultimate tensile strength are improved when Ni is substituted by any alloying element, but that the elongation is decreased by this substitution except for Cr.
Effects of solid solution hardening and precipitation hardening were separately evaluated in Table 8. Clearly W is the most effective in solid solution hardening, while Ta, which is a gamma-prime former and has the largest coefficient in Table 7, is less effective than W as a solid solution hardening element.

4.3. Hot corrosion resistance

Hot corrosion resistance was evaluated by crucible test , keeping a piece of alloy (6-8 mm in diameter and 3-5 mm in height) in a salt mixture (Na₂SO₄-25%NaCl) open to air at 900 deg.C for 20h. The resistance was quantitatively specified by metal loss after all the scales being removed. Morphologically the hot corrosion was classified into three types ; Type I : corrosion layer composed of Cr sulfide, Ni sulfide, and porous oxide, TypeII : corrosion layer of thin tight Cr₂O₃ with a slight or no amount of sulphide in matrix, Type III : corrosion layer composed of three layers of oxides, Cr₂O₃, TiO₂, and Al₂O₃ from outside to inside with a little amount of Cr rich sulphide dispersed in matrix.
A regression analysis was carried out over 42 alloys giving type I corrosion. The resultant equation is shown in Table 9 (For comparison sake another regression equation is shown in the same table for a burner rig test conducted elsewhere[l9] ; both equations show a good agreement except for Nb). The equation indicates that Hf doped and a high Cr and Ti containing alloy is the most preferable in gamma-prime precipitation hardening alloys, while the addition of W, Ta, or Mo, which are essential for increase of high temperature strength, is extremely harmful for the hot corrosion.
The equation does not give a good prediction of other types of hot corrosion than type I. This means that there is(are) other factorts) to govern the hot corrosion. Although it is not clear what they are, our experiment has suggested that content of Ti plays an important role.

Table 1. Equation of gamma-prime surface as a function of gamma-prime composition (at%), obtained by regression analysis. Probability (%) of error of the analysis is smaller than 0.5 and that of each coefficients is smaller than 0.1.

Table 2. Partitioning ratios as functions of gamma-prime composition (at%) and as constants.

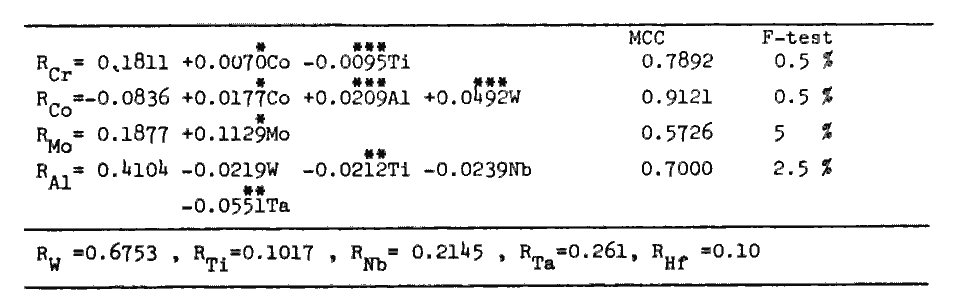
Table 3. Regression analyses of solidus and liquidus temperatures (deg.C).

Table 4. regression analyses of creep rupture strength (kgf/mm²) as functions of gamma (gamma) composition (at%) and gamma-prime volume fraction (vol%).

Table 5. Compositions of typical alloys developed and those of the strongests in commercial alloys, with their strengthening factors..

Table 6. Regression analysis of creep rupture life (h) at 1000 deg.C and at 117.6N/mm².

Table 7. Regression analysis of tensile properties, showing the effects of alloy composition (at%) and heat treatment.

Table 8. Regression analysis of tensile properties, showing the effects of solid solution hardening, precipitation hardening, and heat treatment.

Table 9. Comparison of regression analyses of two hot corrosion tests. 1) log[metal loss(mm/20h)] and 2) log[corrosion rate(IN-738=1)] are calaulated for an alloy composition (at%)..

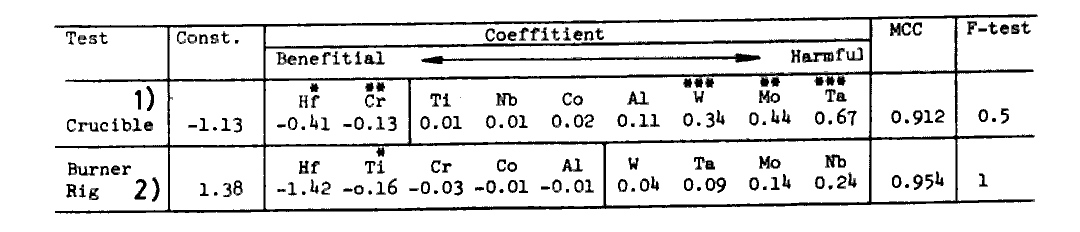
Fig.1 Schematic flow chart for search alloys with desired properties. All the possible compositions are examined at given gamma-prime volume fraction (f) and C, B, and Zr concentrations. Variations of the flow are possible.

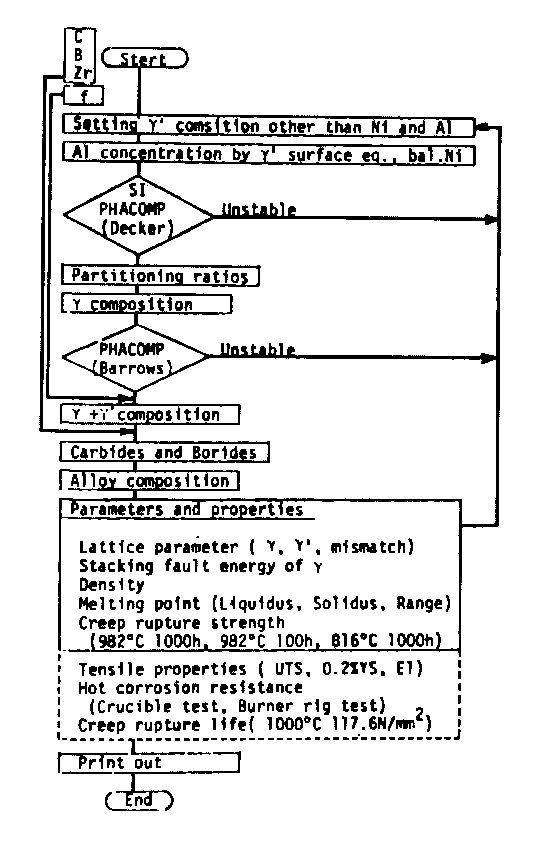
Fig.2 Schematic phase diagram, showing a gamma-prime surface. A and B are substitutional solid solutioning elements, Cr, Ti, W, Ta, etc.

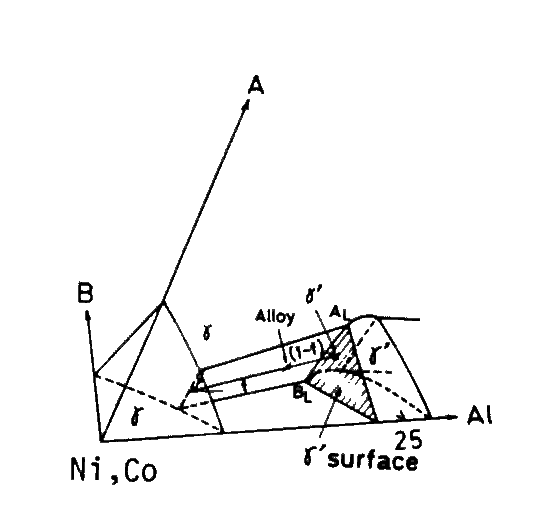
Fig.3 Structures of grain boundary areas of six alloys with various fractions of gamma-prime,after aging (1000 deg.C x 200h, W.Q.) ; etched in glyceregia and observed in SEM.

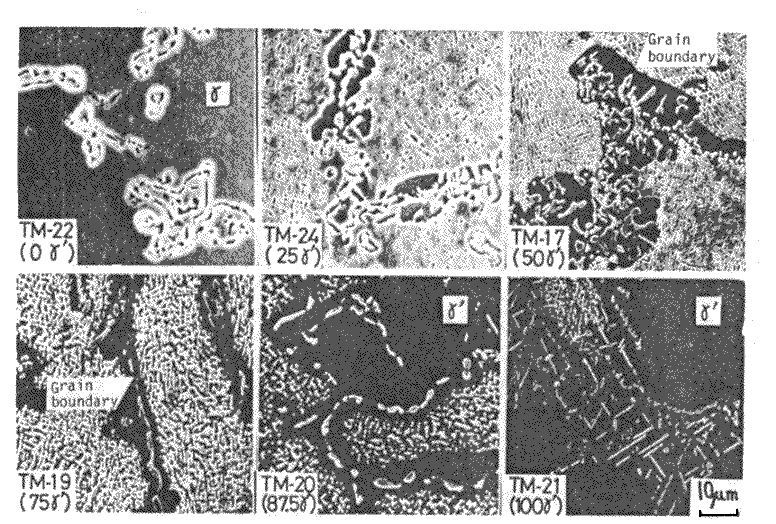
Fig. 4 Relation between designed and measured amounts of gamma-prime, after aging(1000 deg.C x 200h,W.Q.), showing good agreement of total amounts.
Maximum gamma-prime precipitate(gamma-prime p) is obtained when total gamma-prime is 62.5 to 75 vol%. (gamma-prime GB: Grain boundary gamma-prime, gamma-prime N: gamma-prime nodule or primary gamma-prime)

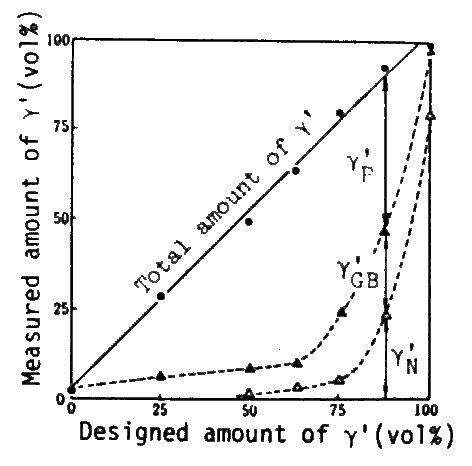
Fig. 5 Creep rupture strength as a funtion of gamma-prime volume fraction.
Maximum strength is obtained when designed amount of gamma-prime is 62.5 to 75 vol%.

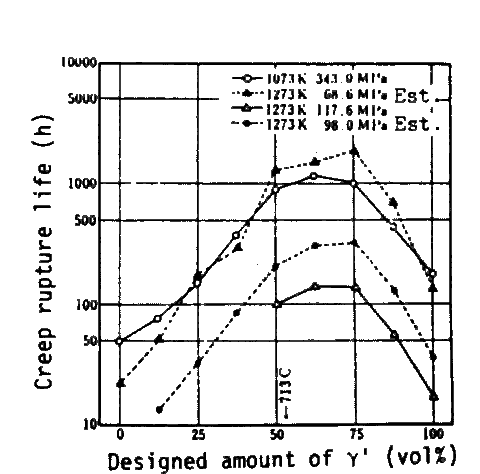
Fig. 6 Schematic phase diagram, showing the composition range in which the alloys designed are lying.

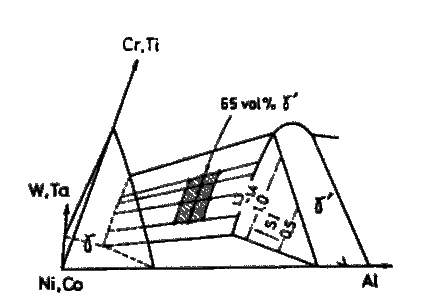
Fig. 7 Comparison of alloys developed and commercial ones, form two properties, creep rupture strength and hot corrosion resistance. Tensile elongation at 900 deg.C is also shown in ( ). TM-210 needs surface removal.

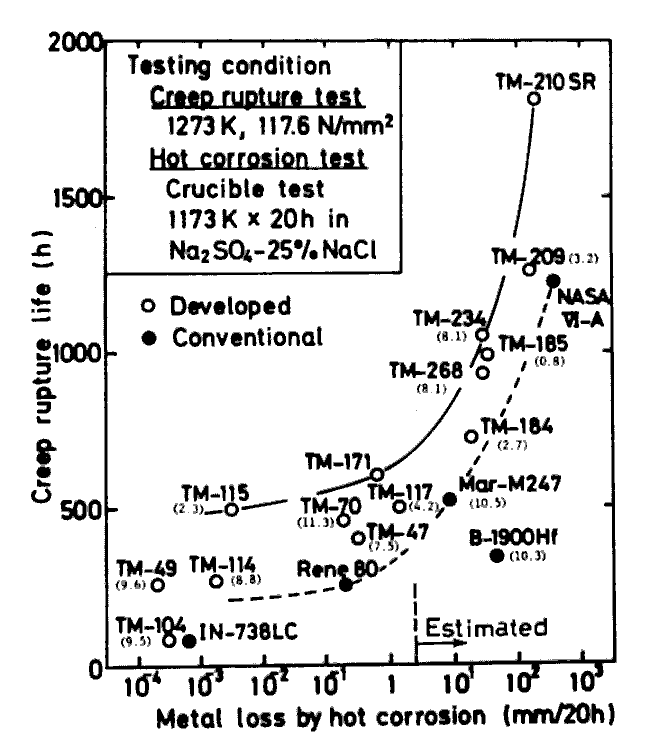
Fig. 8 Creep curves of two conventionally cast alloys and their modifications for a single crystal, at 982 deg.C and at 200N/mm2.

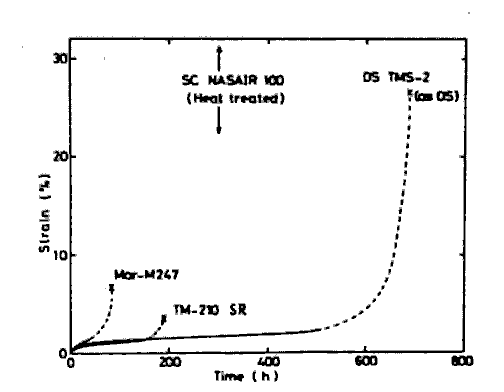
Fig. 9 Creep rupture lives of several series of alloys developed, as a function of gamma-prime volume fraction.

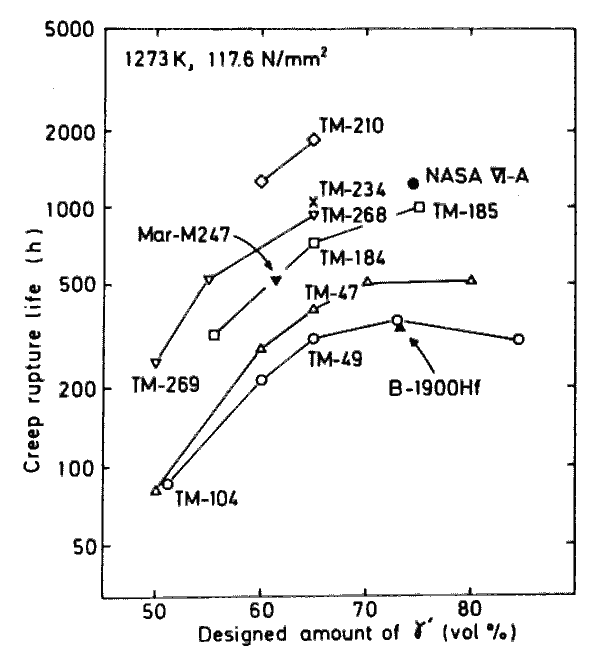
Fig. 10 gamma-prime -fraction dependance of tensile properties, showing that all the properties are the linear funtions of gamma-prime fraction.

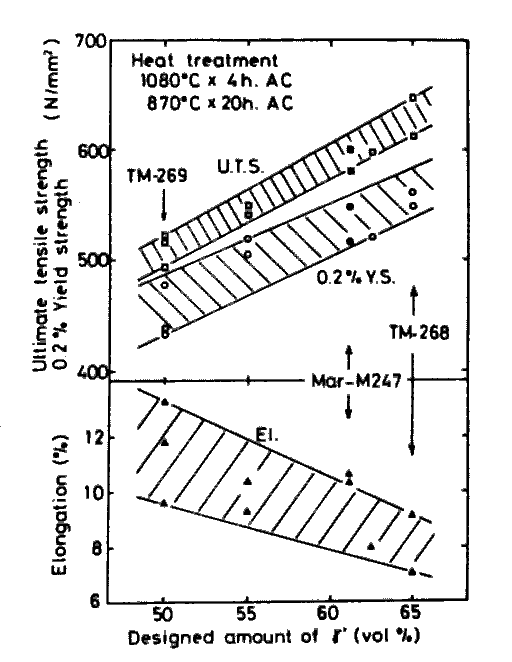
Fig. 11 Tensile properties as funtions of solution temperature, showing that the elongation and 0.2%Y.S. are strong linear funtions of solution temperature.

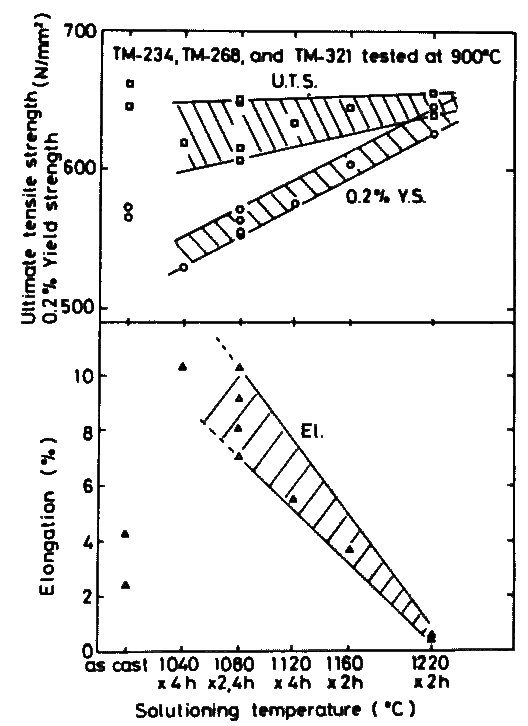
Fig. 12 Comparison of grain boundary structures of an alloy TM-234, after heat treatments With a lower solution temperature (1080 deg.C), a slight amount of gammaprime is solutioned and precipitated as a fine gamma-prime, but a number of fine particles of W rich carbide precipitate at grain boundaries.

5. References

[1] H.Harada and M.Yamazaki: Tetsu-to-Hagane,65(1979),l059.
[2] H.Harada, M.Yamazaki, and Y.Koizumi: Tetsu-to-Hagane,65(1979), l049.
[3] O.H.Kriege and J.M.Baris: Trans,ASM,62(1967),195.
[4] J.E.Restall and E.C.Toulson: Metals and Materials,March(1973),134,April,187. (Part I and II)
[5] R.F.Decker: Symposium on Steel Strengthening Mechanisms,May (1969), Greenwich, U.S.A.,147.
[6] H.Harada et al.: Trans. Iron & Steel Inst. of Japan(I.S.I.J.), 21(1981), B-249.
[7] R.G.Barrows and J.B.Newkirk: Met. Trans.,3(1972),2889.
[8] Y.Koizumi, M.Yamazaki, and H.Harada: Trans.NRIM,19(1977),344.
[9] Constitutions of binary alloys(M.Hansen, R.P.Elliot, and F.A.Shunk)
[10] INCO," High temperature high strength nickel-base superalloys" July(1977).
[11] M.C.Hebeisen et al.: NASA-SR-5095,125.
[12] H.Harada et al.: Trans. I.S.I.J.,21(1981),B-379.
[13] H.Harada et al.: Trans. I.S.I.J.,21(1981),B-380.
[14] A.Takei et al.: Boshoku-Gijutsu,31(1982),208.
[15] A.Takei et al.: Boshoku-Gijutsu,31(1982),218.
[16] Y.Ro et al.: Trans. I.S.I.J.,21(1981),B-530.
[17] Y.Ro et al.: Trans. I.S.I.J.,22(1982),B-70.
[18] T.E.Strangman et al.:"superalloys '80",proceedings of the 4th International symposium,seven springs,l980,215.
[19] P.Huber:"High temperature alloys for gas turbines", proceedings of a conference(COST 50), Liege,1978,251.